Johannes Kepler
De Wikisofia
Avís: El títol a mostrar «Johannes Kepler» sobreescriu l'anterior títol a mostrar «Kepler, Johannes».
Astrònom alemany, nascut a Weil der Stadt, en Würtemberg, fill –hemofílic i miop– d'un soldat de fortuna, Heinrich Kepler, i de Katherine Guldemann, la seva dona, que el seguia en la guerra. Després de cursar els seus estudis a l'escola popular del convent de Maulbronn, una beca li permet estudiar, dels 13 als 16 anys, en el seminari de Tubinga. Als 20, es gradua a la universitat de Tubinga i estudia després teologia, que abandona per un lloc de matemàtic i astrònom en Graz, que se li ofereix en 1594. Es dedica inicialment a les prediccions astrològiques i als horòscops, malgrat considerar-los «sortilegis i fetilleries», però concep al mateix temps la possibilitat d'una nova astronomia, cosa que persegueix, en un primer moment, per la via del misteri i dels símbols.
En Mysterium Cosmographicum (1596) (El títol sencer del qual és: Un avanç (prodromus) d'un Tractat Cosmogràfic, que conté el Misteri Còsmic de les admirables proporcions entre les Òrbites Celestes i les autèntiques i distintives raons per als seus Nombres, Magnituds i Moviments Periòdics, per Johannes Kepler, matemàtic de l'il·lustre Estat d'Estiria, Tubinga any 1596.), obra que, encara que de caràcter simbòlic mostra genialitat, intenta mostrar la relació existent entre les distàncies dels planetes al Sol i el temps de rotació, que no era simplement proporcional a la distància, sinó major, atès que en augmentar la distància disminuïa la velocitat. Creu descobrir la llei establint una relació entre els sòlids regulars platònics i les distàncies dels planetes al Sol, inscrivint aquests sòlids en successives esferes: cub, tetraedre, dodecaedre, icosaedre i octaedre, de manera que l'esfera de Saturn quedava circumscrita a un cub en el qual s'inscrivia l'esfera de Júpiter, que circumscrivia el tetraedre, etc. Seguint aquest ordre: Saturn – cub – Júpiter –tetraedre – Mart – dodecaedre – Terra – icosaedre – Venus – octaedre – Mercuri.
Aquesta obra, malgrat la seva aparença místico-pitagòrica, era la primera acceptació pública i argumentada del sistema de Copèrnic, feta per un astrònom; partia del supòsit, en la seva primera part, que, ja que el món és perfecte i no existeixen sinó cinc sòlids perfectes, havia d'haver-hi una relació entre una cosa i una altra. Però la segona part de l'obra intenta provar amb demostracions geomètriques el plantejament que considera només «probable» de la circumscripció de les òrbites segons els sòlids regulars i del gir de la Terra entorn del Sol, i aquestes demostracions matemàtiques es consideren el planter de la nova teoria astronòmica que ell mateix anava a fundar.
El llibre li va donar a conèixer en tota Europa i, sobretot, va cridar l'atenció de Tycho-Brahe, que en 1600, li va encarregar que continués els seus treballs.
A causa de la persecució religiosa, Kepler, luterà, va ser expulsat de Graz. Aprofitant el viatge del baró Hoffmann, de Graz a Praga, que li va acceptar en el seu seguici l'1 de gener de 1600, Kepler va poder posar-se en contacte amb Tycho-Brahe, qui li va encarregar investigar l'excentricitat de l'òrbita de Mart.
Nomenat matemàtic imperial a la mort de Tycho-Brahe, en 1601, roman a Praga fins a 1612, any de la mort de Rodolf II. En aquest temps funda l'òptica –que va anomenar diòptrica– i l'astronomia física.
La seva gran obra d'astronomia, Nova astronomia o Física del cel (1609) (El títol original del qual és: Astronomia nova Αιτιολογητοσ, seu Physica coelestis tradita comentariis de motibus stellae Martis, Ex observationibus G.V. Tychoniis Brahe), assenyala l'inici de l'astronomia moderna. Presenta les dues primeres lleis de Kepler (la tercera la publicarà en Harmonices Mundi, 1619. (Veg. la formulació de les lleis de Kepler més avall)
Atribueix el moviment del sistema solar a una força «magnètica i material molt simple», que exerceix el Sol sobre els planetes.
A l'any següent pot assabentar-se dels descobriments que Galileu duu a terme amb el seu telescopi, i que narra en el Sidereus Nuncius (1610), i sobre els quals Galileu li demana l'opinió. Sobre aquestes observacions escriu Kepler Conversa amb el missatger dels estels, com a carta (laudatòria i retòrica) a Galileu.
Al setembre d'aquest mateix any, gràcies al telescopi prestat per un matemàtic imperial, va poder Kepler contemplar els planetes medicieus. Sobre això va escriure Informe de les observacions dels quatre satèl·lits errants de Júpiter, primer reconeixement oficial que un astrònom feia dels descobriments de Galileu. Aquest, en canvi, va ignorar fins a la fi dels seus dies les lleis de Kepler.
Dioptrice (1610), que vol dir «refracció», és l'obra en la qual Kepler, completant una obra anterior, Ad Vitellionem paralipomena (1604), desenvolupa correctament els principis de l'òptica geomètrica i instrumental, encara que sense arribar a formular la llei de la refracció de la llum.
En 1611, després de la mort de l'emperador Rodolf, el rei que s'havia educat a Espanya, de la dona de Kepler i d'un dels seus fills, iniciades ja les lluites intestines entre els Habsburg, que donaran lloc a la Guerra dels Trenta Anys, es trasllada a Linz, a Àustria, amb el càrrec de matemàtic provincial. Allí va haver de suportar l'ominós procés per bruixeria iniciat contra la seva mare, que es trobava en Leonberg, població propera a la seva ciutat natal de Weilderstad, i que va durar de 1615 a 1621. La seva mare va morir poc després d'acabat el procés.
En aquesta època, Kepler escriu Harmonices Mundi Libri V (1619), obra en què intenta la síntesi final de la seva visió cosmològica: l'harmonia –en el més pur sentit pitagòric– total entre la geometria, la música i l'astronomia. En ella formula la tercera llei de Kepler (veg. citació). Publica encara un comentari al sistema copernicà, amb el títol de Epitome Astronomiae Copernicanae (1621), i les Taules Rudolfines, obra d'astronomia pràctica, útils per a l'astrònom i l'astròleg i com a calendari i guia per a la navegació, que segons testimoniatge del mateix Kepler va estar construint durant 22 anys i que després de nombroses dificultats d'impressió va aconseguir tenir disposades per al mercat anual del llibre de la Fira de Frankfurt de 1627. En aquestes utilitza moltes de les dades observacionals registrades per Tycho-Brahe.
Encara afegeix a aquest conjunt d'obres Somnium, inacabat i sorprenent somni d'un viatge a la Lluna.
Va morir a Ratisbona, en el viatge que emprèn cap a Leipzig, carregat de llibres, però sense la seva segona dona ni els fills, en plena Guerra dels Trenta Anys, a la recerca dels diners que li devia l'emperador.
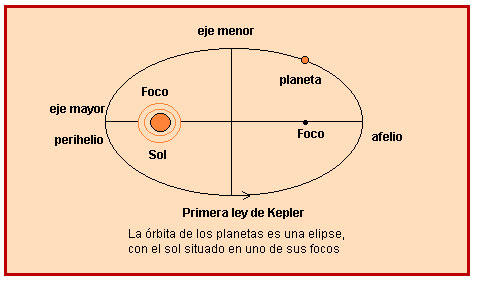
Primera llei: llei de l'el·lipse (1609). L'òrbita de cada planeta és una el·lipse, amb el sol en un dels seus focus.
(Conseqüència: la distància del planeta al sol varia al llarg de l'òrbita)
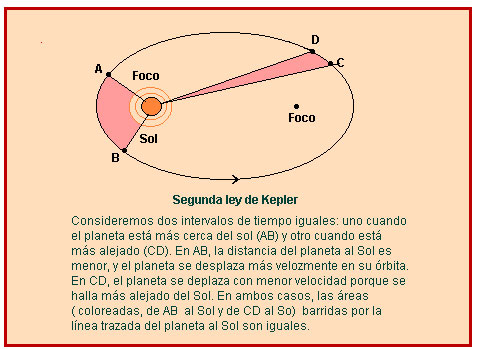
Segona llei: llei de les àrees (1609). Una línia traçada des d'un planeta al sol escombra àrees iguals en temps iguals.
(Conseqüència: la velocitat de desplaçament no és uniforme: a major distància del sol, menor velocitat).
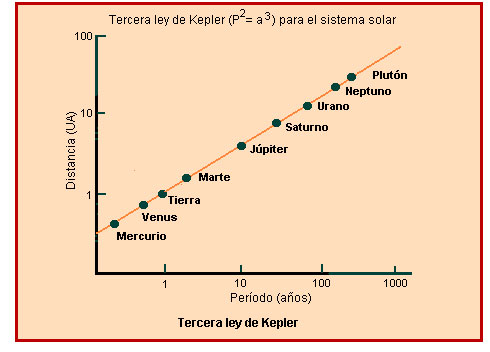
Tercera llei: llei harmònica (1619). El quadrat del període d'un planeta és directament proporcional al cub de la seva distància mitjana al sol.
Algebraicament, [math]\displaystyle{ P^2 = ca^3 }[/math], on P és el període orbital, a la distància mitjana al sol i k una constant.
(Conseqüència: a major òrbita solar, menor velocitat de desplaçament del planeta)
Termes relacionats