Validesa

En els raonaments o arguments deductius, propietat per la qual, si les premisses són veritables, la conclusió ha de ser necessàriament veritable. O bé, condició que fa que és impossible que les premisses siguin veritables i la conclusió falsa.

La validesa d'un raonament no depèn que les premisses siguin de fet veritables, sinó només de la seva forma. La forma ha de ser tal –si és vàlida– que, en el cas que les premisses siguin veritables, la conclusió també ho serà, però si les premisses no ho són, la conclusió pot ser veritable o falsa

veg. exemple ↓

Alguns estudiants estimen la música clàssica

Els que estimen la música clàssica són persones sensibles

___________________________________________

Alguns estudiants són persones sensibles

Aquest raonament sil·logístic té una forma vàlida:

Alguns S són M

Tots els M són P

_______________

Alguns S són P

però si es parteix de premisses falses, la conclusió pot ser falsa:

Exemple:

Alguns homes volen

Tot el que vola és ocell

_______________________

Alguns homes són ocells

exemple

Mentre que en un raonament invàlid la forma és tal que hi ha casos en què, sent veritables les premisses, la conclusió és falsa. A aquests casos se'ls anomena contraexemples.

veg. exemple ↓

La següent forma lògica és invàlida :

Tots els M són P

Alguns S no són M

__________________

Alguns S no són P

Exemple:

Tots els músics són persones sensibles

Alguns savis no són músics

________________________________________

Alguns savis no són persones sensibles

Perquè, encara que en aquest cas tant les premisses com la conclusió són veritables, admet contraexemples:

Contraexemple:

Totes les paraules esdrúixoles s'accentuen

«Anís» i «arcabús» no són paraules esdrúixoles

________________________________

«Anís» i «arcabús» no s'accentuen

On les premisses són veritables i la conclusió falsa.

(veg. exemple)

A un raonament inductiu només impròpiament se'l pot anomenar vàlid, perquè sempre admet la possibilitat que, fins i tot sent veritables les seves premisses, la conclusió sigui falsa. El grau de certesa a què pot arribar la conclusió d'un raonament inductiu és només la probabilitat. En tot cas, del raonament inductiu que té premisses veritables i conclusió probable es diu que és un «bon» raonament inductiu

veg. exemple ↓

El grau de probabilitat de la conclusió és variable, en funció del suport que rep de les premisses:

Exemple:

En tots els Jocs Olímpics es baten diverses marques esportives

___________________________________________________________________

Per tant, en els propers Jocs Olímpics almenys un atleta batrà alguna marca esportiva

Aquesta conclusió és més probable que la del següent raonament:

En tots els Jocs Olímpics es baten diverses marques esportives

_____________________________________________________________________

Per tant, en els propers Jocs Olímpics algun atleta català batrà alguna marca esportiva

Recurs:Raonament inductiu i probabilitat

Per als raonaments deductius de lògica d'enunciats es disposa d'un mètode eficaç per a provar la seva validesa: les taules de veritat que analitzen els valors de veritat de les fórmules que constitueixen premisses i la conclusió, de manera que, pel seu mitjà, es posa també de manifest la definició de validesa: si sempre que les premisses són totes elles veritables la conclusió també ho és, el raonament –formal, en aquest cas– és vàlid

veg. exemple ↓

Sigui el següent raonament:

«Si somio, desitjo, i si estic despert, em deleixo, i o somio o estic despert; per tant o desitjo o em deleixo», la formalització del qual pot ser:

[math]\displaystyle{ [[(p\rightarrow q)]\wedge (r\rightarrow s)]\wedge (p\vee r)]\rightarrow q\vee s }[/math]

la taula de veritat d'aquest «dilema constructiu» és la següent:

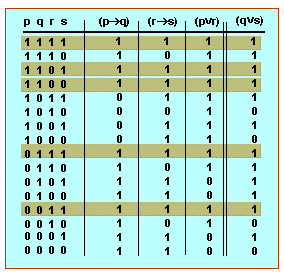
La taula mostra que, sempre que les premisses són vertaderes, la conclusió també és vertadera, i no succeeix que les premisses siguin vertaderesi la conclusió falsa. La taula mostra que el «dilema constructiu» és un raonament vàlid.

Recurs:Taula de veritat d'un raonament

La validesa es refereix pròpiament als raonaments, però pot també referir-se a un enunciat, o fórmula d'enunciat. Qualsevol fórmula que resulta veritable per tota assignació de valors de veritat a les seves lletres d'enunciat, o per tota interpretació, és una fórmula universalment vàlida; una fórmula vàlida és una expressió lògicament veritable o una tautologia.

veg. exemple ↓

Pot provar-se la validesa del raonament anterior (veg. exemple) mostrant, amb les taules, que el condicional format per les premisses i la conclusió és una tautologia

Recurs:Taula de veritat d'una tautologia

---

La correcció -o validesa- d’un argument no depèn, doncs, de que els enunciats que el componen siguin, de fet, verdaders o falsos, sinó de si, entre premisses i conclusió, existeix conseqüència lògica. Així, per exemple, pot haver-hi un raonament completament vàlid a partir de premisses falses.

Per exemple:

«Tots els americans són bevedors de Coca Cola, i tots els bevedors de Coca Cola mengen crispetes; per tant, tots els americans mengen crispetes.»

Aquest raonament és vàlid (està lògicament ben construït), però ni les premisses són verdaderes (evidentment hi ha molts americans que no beuen Coca Cola, ni és veritat que tots els que beuen Coca Cola siguin menjadors de crispetes), ni tampoc no és verdadera la conclusió (ja que, certament, no tots els americans mengen crispetes). Per tant, és vàlid, però la conclusió no és verdadera. De fet l’exemple següent és estructuralment idèntic a l’anterior:

«Tots els Hunguis són Xunguis, i tots els Xunguis són Fus, per tant.... tots els Hunguis són Fus.»

Està clar que en aquest cas en comptes de parlar, com en l’exemple anterior, d’americans, Coca Cola i crispetes, hem posat Hunguis, Xunguis i Fus (termes completament inventats), però l’estructura o forma és la mateixa. En general, si prescindim del significat i ens centrem solament en la forma, aquest exemple quedaria de la manera següent:

«Tots els A són B, i tots els B són C, per tant.... tots els A són C»

Intuïtivament veiem que és una forma correcta o vàlida independentment del seu contingut. Aquí A, B i C substitueixen els continguts anteriors ("Americans", "Hunguis", etc.). En aquest sentit diem que la lògica és una ciència formal, és a dir, que prescindeix dels continguts i es queda solament amb l’estructura dels raonaments o argumentacions.

En certa forma ens podem imaginar la lògica com un recipient, i els seus continguts com el líquid que l’omplen. Ens podem preguntar, per exemple, de quina forma és el vi, o la cervesa, o l’aigua? La resposta ens la dona el recipient. Si el recipient és cúbic, llavors el vi, o l’aigua o la cervesa, etc., són cúbics, ja que estan obligats a seguir la forma del recipient. Si, en canvi, el recipient és cilíndric, llavors el seu contingut ha de seguir necessariament la forma cilíndrica, etc. El recipient, doncs, determina la forma. En aquest sentit -seguint l’analogia-, si un raonament (indistintament de si tracta de "tal" o si tracta de "qual") ha de seguir unes determinades formes lògiques. Si segueix una forma correcta, llavors els raonament és també correcte o vàlid. En cas contrari és invàlid o no vàlid.

Ara bé, la validesa és una propietat purament formal (que depèn de la forma), mentre que la veritat és una propietat dels enunciats en la seva relació amb els fets. Si un raonament és formalment vàlid, i les seves premisses són verdaderes, llavors la conclusió serà necessàriament verdadera.

Cal, doncs, no confondre veritat i validesa. Una cosa és que la conclusió sigui verdadera i una altra que la seva deducció sigui vàlida. Una cosa és la veritat de les premisses i la veritat de la conclusió (problema filosòfic complicat que, com hem dit fa referència a la relació entre el significat del enunciats i els fets que aquests descriuen), i una altra la validesa del raonament que, com acabem de dir és solament una propietat formal.

• La veritat de les premisses depèn, segons la teoria de la correspondència, de si el que l’enunciat diu és, en realitat, allò que succeeix.

• La validesa del raonament depèn de si la conclusió és una conseqüència lògica de les premisses.

• La validesa depèn de la forma com s’argumenta i no del contingut de veritat o falsedat els seus enunciats.

És a dir, es pot ser un bon lògic dient coses falses, però ben estructurades... Però no es pot ser un bon investigador de la realitat si no es segueixen les regles de la lògica. Un científic, o un advocat, o un economista, etc., poden saber molt del seu camp, però si no articulen els seus pensaments i raonaments segons les formes lògiques adequades... llavors el seu pensament no val res. Així, doncs, certament, la lògica no serveix per descobrir la veritat, però si hom no segueix les seves regles, per més que parteixi de veritats, no arribarà a conclusions ben fonamentades.

• En resum. es pot ser un bon lògic dient tonteries i/o coses falses? Resposta: sí

• Es pot ser un bon científic, o un bon advocat, o un bon polític argumentant segons formes lògiques no vàlides? Resposta: no (Almenys si entre els teus adversaris hi ha algú que sàpiga lògica)

Així, doncs, la lògica és una disciplina que cal seguir per tal d’assegurar que hom articula bé els pensaments de qualsevulla disciplina que s’estudiï.

Un enunciat és conseqüència lògica de les premisses si és impossible que les premisses siguin verdaderes i la conclusió falsa. Això depèn únicament de la forma del raonament i no de cap veritat de fet.

Diem, doncs, que un raonament és vàlid -formalment correcte- quan la seva forma és tal que sempre que les premisses són verdaderes la conclusió també ho és, o bé quan és impossible que les premisses siguin verdaderes i la conclusió falsa. I sempre i en tot cas, la validesa d’un raonament no depèn de la veritat o falsedat de les premisses. Si el raonament és vàlid i, a més, les seves premisses són verdaderes, el raonament és també materialment correcte, això és, un raonament sòlid.

En els raonaments vàlids, les premisses impliquen la conclusió. I llavors, les premisses i la conclusió són necessàriament consistents.

També es pot dir que un raonament és vàlid si no té contraexemples.

En conclusió, només si raonem correctament, estem legitimats a utilitzar l’expressió «per tant», i d’altres expressions equivalents.

---

Veg. Forma_vàlida i fórmula universalment vàlida.