Tautologia

(ταυτολογία del grec τάυτό, tautó, el mateix, i λόγος, logos, terme)

Literalment, dir el mateix dues vegades. En sentit ampli, tota proposició analítica o tot enunciat (explícitament) analític, és a dir, qualsevol d'aquells enunciats analítics que ho són en virtut de la seva forma, no pel significat dels seus termes.

En sentit estricte, és una veritat lògica, o una veritat formal, o aquell esquema lògic o aquella forma lògica, els exemples de la qual de substitució són tots veritables.

En sentit ampli, és una tautologia dir que «els lladres són amants de l'aliè», perquè és una veritat analítica, però és una tautologia estricta dir que «una llar és sempre una llar», perquè és un exemple de substitució d'un esquema formal que, en lògica d'enunciats, s'escriu [math]\displaystyle{ p\rightarrow{p} }[/math]

Exemple

«Vencerem o no vencerem» és una tautologia, que pot escriure's
[math]\displaystyle{ q\vee ¬q }[/math]
i és per tant veritable per la seva forma lògica; en canvi, «Ets pare, si ets home mentre que ets mare, si ets dona» és un enunciat analític no tautològic.

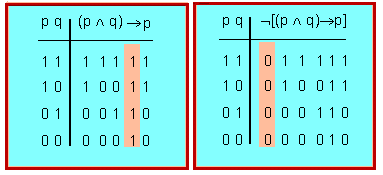
Les tautologies són veritats lògiques i la seva negació constitueix una contradicció (veg. text).

En el càlcul lògic d'enunciats, una fórmula és tautològica si és veritable per a qualsevol assignació de valors de veritat, o per a qualsevol interpretació. Igualment, la negació d'una fórmula tautològica és una contradicció.

Exemple

[math]\displaystyle{ (p\wedge q) \rightarrow{p} }[/math]
és una tautologia;

[math]\displaystyle{ ¬[(p\wedge q) \rightarrow{p}] }[/math]
és una contradicció.