Validesa
De Wikisofia
La revisió el 15:40, 25 abr 2015 per Jorcor (discussió | contribucions) (Text de reemplaçament - "File:i" a "File:e")
En els raonaments o arguments deductius, propietat per la qual, si les premisses són veritables, la conclusió ha de ser necessàriament veritable. O bé, condició que fa que és impossible que les premisses siguin veritables i la conclusió falsa.
La validesa d'un raonament no depèn que les premisses siguin de fet veritables, sinó només de la seva forma. La forma ha de ser tal -si és vàlida- que, en el cas que les premisses siguin veritables, la conclusió també ho serà, però si les premisses no ho són, la conclusió pot ser veritable o falsa
- Alguns estudiants estimen la música clàssica
- Els que estimen la música clàssica són persones sensibles
- ___________________________________________
- Alguns estudiants són persones sensibles
Aquest raonament sil·logístic té una forma vàlida:
- Alguns S són M
- Tots els M són P
- _______________
- Alguns S són P
però si es parteix de premisses falses, la conclusió pot ser falsa:
Exemple:
- Alguns homes volen
- Tot el que vola és au
- _______________________
- Alguns homes són aus
Mentre que en un raonament invàlid la forma és tal que hi ha casos en què, sent veritables les premisses, la conclusió és falsa. A aquests casos se'ls anomena contraexemples.
La següent forma lògica és invàlida :
- Tots els M són P
- Alguns S no són M
- __________________
- Alguns S no són P
Exemple:
- Tots els músics són persones sensibles
- Alguns savis no són músics
- ________________________________________
- Alguns savis no són persones sensibles
Perquè, encara que en aquest cas tant les premisses com la conclusió són veritables, admet contraexemples:
Contraexemple:
- Totes les paraules esdrúixoles s'accentuen
- «Anís» i «patatús» no són paraules esdrúixoles
- ________________________________
- «Anís» i «patatús» no s'accentuen
On les premisses són veritables i la conclusió falsa.
A un raonament inductiu només impròpiament se li pot anomenar vàlid, doncs sempre admet la possibilitat que, àdhuc sent veritables les seves premisses, la conclusió sigui falsa. El grau de certesa al fet que pot arribar la conclusió d'un raonament inductiu és només la probabilitat. En tot cas, del raonament inductiu que té premisses veritables i conclusió probable es diu que és un «bon» raonament inductiu
El grau de probabilitat de la conclusió és variable, en funció del suport que rep de les premisses:
Exemple:
- En tots els Jocs Olímpics es baten diverses marques esportives
- ___________________________________________________________________
- Per tant, en els propers Jocs Olímpics almenys un atleta batrà alguna marca esportiva
Aquesta conclusió és més probable que la del següent raonament:
- En tots els Jocs Olímpics es baten diverses marques esportives
- _____________________________________________________________________
- Per tant, en els propers Jocs Olímpics algun atleta espanyol batrà alguna marca esportiva
Per als raonaments deductius de lògica d'enunciats es disposa d'un mètode eficaç per provar la seva validesa: les taules de veritat que analitzen els valors de veritat de les fórmules que constitueixen premisses i la conclusió, de manera que, pel seu mitjà, es posa també de manifest la definició de validesa: si sempre que les premisses són totes elles veritables la conclusió també ho és, el raonament -formal, en aquest cas- és vàlid
Sigui el següent raonament:
«Si somni, desig, i si estic despert, anhelo, i o somni o estic despert; per tant o desig o anhelo», la formalització del qual pot ser :
la taula de veritat d'aquest «dilema constructiu» és la següent:
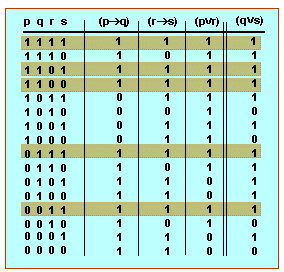
La taula mostra que, sempre que les premisses són veritables, la conclusió també és veritable, i no succeeix que les premisses siguin veritables i la conclusió falsa. La taula mostra que el «dilema constructiu» és un raonament vàlid.
La validesa es refereix pròpiament als raonaments, però pot també referir-se a un enunciat, o fórmula d'enunciat. Qualsevol fórmula que resulta veritable per tota assignació de valors de veritat a les seves lletres d'enunciat, o per tota interpretació, és una fórmula universalment vàlida; una fórmula vàlida és una expressió lògicament veritable o una tautologia.
Pot provar-se la validesa del raonament anterior (veure exemple) mostrant, amb les taules, que el condicional format per les premisses i la conclusió és una tautologia