Paradoxes de Zenó
De Wikisofia
Primeres paradoxes de la història del pensament, atribuïdes a Zenó d'Elea, i transmeses sobretot a través de la Física d'Aristòtil. Deixeble de Parmènides, fins a fill adoptiu o potser amant, Zenó va divulgar la idea de la impossibilitat del moviment, o del canvi, mitjançant diversos raonaments sofístics i argumentacions paradoxals, de les quals les més conegudes són quatre (però, pel que sembla, van arribar a ser més de quaranta), basades totes elles en l'argument (o arguments) contra la pluralitat: la paradoxa d'Aquil·les i la tortuga, la paradoxa de la dicotomia, la de la fletxa en vol, i la paradoxa de l'estadi.
Argument contra la pluralitat
Zenó s'oposa a la pluralitat i a la divisibilitat de les coses, tal com l'entenien els pitagòrics, amb diversos arguments, transmesos per fragments conservats, sobretot, en la Física d'Aristòtil i els Comentaris a la física d'Aristòtil de Simplici. Tant l'espai com les coses mateixes no poden ser ni divisibles ni plurals; als ulls de la raó no existeixen «moltes» coses, i tot és «un». En efecte, les coses no són divisibles, perquè, si ho anaven, o estarien formades per elements infinitament divisibles i inextensos o d'un nombre finit d'elements extensos. En el primer cas, la cosa mateixa sencera mancaria d'extensió, perquè l'infinitament petit –segons Zenó, que desconeixia la suma finita d'una sèrie de valors infinitament petits– és igual a zero. En el segon cas, la cosa sencera mateixa seria infinitament gran, perquè, què pot separar dos elements finits? Altres elements finits. I aquests, al seu torn, com poden separar-se? Per altres elements finits, i així fins a l'infinit (no es coneixia encara el buit). Infinit nombre d'elements finits separats donen un total, per a qualsevol cosa, de dimensions infinites. L'argument tendeix a mostrar que, suposada la pluralitat i la divisibilitat, s'arriba a conclusions contràries (elements finits, elements infinits; coses inextenses, coses de dimensions infinites), ambdues rebutjables. El món és, doncs, malgrat les aparences, un, continu, compacte, tal com deia Parmènides (vegeu el text).
A la base d'aquesta argumentació, està el fet que Zenó desconeixia l'existència del buit i, sobretot, el valor finit d'una suma de valors infinitament petits, confonent així l'infinit matemàtic amb la divisibilitat material o, en tot cas, argumentava a partir de la dificultat d'explicar com una sèrie infinita de passos o instants poden sumar-se en una sèrie finita.
En un altre argument semblant, conegut amb el nom de paradoxa dels grans de mill, relatat per Simplici, ataca la divisibilitat tocant al so, portant també les matemàtiques pitagòriques al terreny de la física i el material, en aquest cas, en l'aspecte de la teoria musical: un sol gra de mill, en caure, no fa soroll, ni en fa tampoc una mil·lèsima part de gra; però sí que fan soroll en caure mil grans de blat. És que els sons no poden relacionar-se entre si com els objectes que causen els sons? On està, doncs, el fonament de la teoria musical dels pitagòrics, que relacionaven les proporcions matemàtiques amb les proporcions de les cordes en tensió?
Aquil·les i la tortuga
La paradoxa d'Aquil·les és el segon argument contra el moviment. El semidiós Aquil·les, el més veloç dels grecs, aposta una carrera amb un dels més lents animals terrestres, la tortuga. El guerrer (A) atorga magnànim un avantatge al quelonio, que parteix des del punt T. Quan Aquil·les arribi a aquest punt, la tortuga, suposa Zenó, haurà aconseguit un altre avantatge (a), i encara que Aquil·les arribi aviat a aquest punt, queda encara un altre avantatge més aconseguit per la tortuga; i així infinitament (vegeu el text). Aquil·les no pot, amb tots els seus treballs, aconseguir a la tortuga.
La dicotomia
Els mals d'Aquil·les són pitjors del previst, si es té en compte que, per la paradoxa de la dicotomia, en realitat ni tan sols pot moure's (Aristòtil, Física, VI, 9, 239b 9) o, en el millor dels casos, no és capaç ni tan sols de competir amb si mateix en l'estadi (vegeu el text).
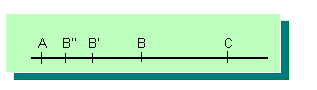
Per a arribar, partint d'un punt inicial (A) a un altre punt determinat (C), Aquil·les o qualsevol cos en moviment, ha de travessar abans el punt mitjà de l'espai existent (B). Per a arribar a aquesta meitat de camí, ha de passar abans pel punt mitjà d'aquesta distància (B; i per a arribar a aquesta nova meitat de camí de l'anterior, ha d'arribar també al punt mitjà d'aquesta distància (B'; i així indefinidament, raó per la qual no és possible que Aquil·les, o qualsevol cos en moviment, en realitat es mogui.
La fletxa
Tercera de les paradoxes de Zenó que ens ha transmès, entre d'altres, Aristòtil (Física VI, 9, 239b 5-7). Part del supòsit que un cos en repòs ocupa un espai «igual a si mateix». Ara bé, una fletxa en moviment ocupa també, per a cada instant, un espai igual a ella mateixa; per tant, està en repòs (vegeu el text).
L'estadi
Quart argument paradójicocon que Zenó, en dir d'Aristòtil (Física VI, 9, 239b 33) rebat la possibilitat de moviment. Es basa, igual que els anteriors, en el supòsit pitagòric que l'espai i el temps es componen d'elements mínims puntuals i indivisibles. Parla de dos «cossos sòlids» o «masses» compostes d'aquests elements puntuals, i que creuen el seu moviment en un estadi, passant per davant d'una altra massa igualment composta del mateix nombre d'elements. Partint d'una posició inicial (I) s'arriba a la definitiva (II), després del moviment.
Els cuerposB i C tenen moviments contraris, però velocitats iguals. En passar de la posició inicial (I) a la posició d'arribada (II), han realitzat un moviment contrari, de tal manera que, per a cada instant, tan puntual i mínim com els mateixos elements components de les masses A, B i C, mentre el cos de B passa per davant de dos elements de A, utilitzant dos instants, el mateix cos de B passa per davant de quatre elements puntuals de C, utilitzant per a això quatre instants. De manera que els B duen a terme, durant el mateix lapse de temps, dos moviments diferents.
La força de la paradoxa es recolza en suposar que el temps, igual que l'espai, es compon d'elements indivisibles, tal com interpretava Zenó als pitagòrics, per als quals «les coses s'assemblaven als nombres» (vegeu el text).
Tots aquests arguments no pretenen mostrar no només la impossibilitat del moviment, sinó la impossibilitat del moviment i de la divisibilitat, o pluralitat. Qui sostingui una o una altra cosa manca d'arguments racionals i es veu abocat a la contradicció. No és possible conciliar moviment i pluralitat, sense contradir-se. Tals arguments, amb tals suposats, van dirigits contra els pitagòrics, els pluralistes i els atomistes.