Relació
De Wikisofia
La revisió el 14:24, 9 maig 2020 per Jorcor (discussió | contribucions) (Text de reemplaçament - "del ser" a "de l'ésser")
(del llatí relatio, de referre, en el seu sentit d'acostar-se a una altra cosa, o de «pel que fa a», que tradueix el grec pros tí)
En Aristòtil, una de les deu categories de l'ésser, o una de les maneres com es presenta i es pensa l'ésser, aquella precisament que ens permet dir d'una cosa que és «relativa», perquè es refereix a una altra o està en dependència d'una altra cosa (vegeu la citació). En la tradició escolàstica, es discuteix si les relacions són ens reals o ens de raó i si els termes d'una relació han de ser, o no, reals perquè el sigui també la relació. Aquesta tradició distingeix en ella un esse in o un «trobar-se en», com a categoria accidental inherent a la substància, i un esse ad, o un ser «referit a un altre», que és la seva característica definitòria. Així, en l'esse ad d'una relació cal distingir: un terme origen de la relació (ser pare) –terminus a quo–, el fonament de la mateixa (la generació), la relació pròpiament dita (la paternitat) i el terme relacional final –terminus ad quem– o correlatiu (el fill). La teoria metafísica de les relacions es presta a una interpretació segons la qual se suposa que, en les coses, és possible diferenciar el que són d'allò a què es refereixen, o un element o aspecte constitutiu i un element o aspecte relatiu, o bé, un element d'identitat i un altre de diferència, fins a arribar a l'afirmació que «l'ésser és referencial», o que «la realitat és correlacional», segons l'expressió del filòsof espanyol Ángel Amor Ruibal, o les expressions més vagues i més genèriques de «tot individu està immers en un context universal». Aquestes afirmacions excedeixen la d'Aristòtil, qui considera indiscutible l'afirmació que cap substància és relativa. Per a Kant, la relació comprèn la substància i l'accident, la causa i l'efecte i l'acció recíproca entre fenòmens, de manera que tot fenomen no és més que un entramat de relacions (vegeu la citació).
En l'espai només hi ha relacions externes; en el sentit intern, només relacions internes; mancada l'absolut.
I. Kant, Crítica de la raó pura, Analítica transc., Apèndix A 266. (afegit a mà per Kant) (Alfaguara, Madrid 1988, 6a ed., p. 279)
Propietat que es dóna entre objectes. A diferència de les propietats que són de l'objecte, les relacions són propietats que es tenen en relació amb un altre, o respecte d'un altre. Són, doncs, predicats poliàdics, o funcions proposicionals amb més d'un lloc.
- 1. « x és més agradable que i» –Rx–, és un exemple de relació binària o diàdica.
- 2. «x està entre i i z» –Rxyz– és ternària o triàdica.
- 3. ....n-ària o n-àdica.
Lògicament, s'expressen mitjançant un parell ordenat, o parells d'elements presos en un determinat ordre. A aquests parells ordenats se'ls anomena dupla, tripla, quadrupla, i en general, per a n elements en determinat ordre, n-tuples; les relacions són, per aquesta raó, binàries, ternàries, i en general n-àries. Donada una relació binària, o un predicat diàdic, per exemple, «x estima a i», la seva extensió és la relació R, o el conjunt de parells ordenats, on x és el conjunt d'individus que estimen a algú, i i el conjunt d'individus estimats per algú; l'extensió d'aquest predicat, o relació, R, està constituïda pel conjunt de parells ordenats
que fan veritable la funció proposicional Fxy; a aquesta relació se la simbolitza com Rxy. Per això, una relació (R) es defineix també com un predicat l'extensió del qual és un conjunt de parells ordenats.
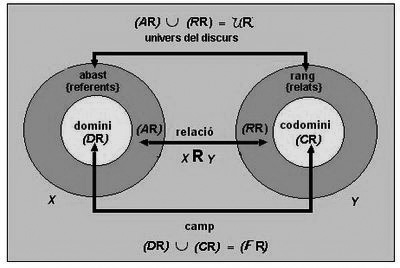
El primer element del parell ordenat x,i rep el nom de referent i el segon, el de relat. Abast [math]\displaystyle{ (A_R) }[/math] és el conjunt de tots els referents, o possibles primers membres del parell ordenat. Rang (RR) de la relació és el conjunt dels seus possibles relats, o segons membres dels parells ordenats. Domini d'una relació binària (DR) és el conjunt de tots els elements x (referents) de l'abast pels quals hi ha almenys un i (relat) del rang que fa veritable la relació; així, en la relació «ser mare de», el domini el forma el conjunt de dones (abast) que tenen algun fill. Contradomini, codomini o domini convers (CR) és el conjunt dels elements i (relats) del parell ordenat pels quals hi ha almenys un x (referent) que fa veritable la relació; en la relació anterior, el contradomini ho constitueixen totes les persones, ja que totes i cadascuna d'elles són fills o tenen mare. Camp d'una relació binària (FR) és la summa lògica de domini i codomini; en la relació «estar casat amb», el camp el forma el conjunt de persones casades, dones i marits. Al seu torn, univers de discurs d'una relació binària (OR) és el conjunt de parells d'individus respecte dels quals té sentit afirmar o no una relació. L'univers de discurs es distingeix de l'extensió d'una relació pel fet que el primer el constitueixen tots els parells ordenats dels quals pot predicar-se una relació, mentre que la segona la formen els parells ordenats que satisfan, o fan veritable, la relació. Quan les relacions estan descrites per enumeració (dels parells ordenats), o quan els individus que pot predicar-se la relació coincideixen amb els quals la satisfan o la fan veritable, el camp d'una relació coincideix amb el seu univers de discurs.
- Per exemple, en el univers del discurs dels homes, la relació "ser marit de" determina les següents classes:
- Domini: els homes casats
- Codomini: les dones casades
- Camp: tots els casats
- Mentre que en univers del discurs dels homes, la relació de "ser de la mateixa espècie que" determina la igualtat de classes entre domini, codomini, camp i univers.
Les principals propietats de les relacions binàries són:
Reflexivitat: Tot element del domini està relacionat amb si mateix. (Exemple: Tothom s'estima a si mateix).
No reflexivitat: la contradictòria de l'anterior. Hi ha almenys un element del camp que no està en relació amb si mateix. (Exemple: Anna admira a Raül).
Irreflexivitat: La contrària de la reflexivitat. Cap element del camp no està en relació amb si mateix. (Exemple: Raül és major que Anna).
Simetria: quan per qualsevol parell d'elements, si el primer es relaciona amb el segon, el segon es relaciona igualment amb el primer. (Exemple: Anna aquesta casada amb Raül).
No simetria: la contradictòria de l'anterior. (Exemple: Anna és germana de Pau (Pau és germà d'Anna).
Asimetria: quan per a tot parell d'elements, si el primer es relaciona amb el segon, el segon no es relaciona amb el primer (la contrària de la simetria). (Exemple: Les Illes Canàries estan al sud d'Europa).
Transitivitat: quan donats tres elements qualssevol, si el primer es relaciona amb el segon i aquest amb el tercer, el primer es relaciona també amb el tercer. (Exemple: Si la lírica és més agradable que l'èpica i l'èpica més agradable que el càlcul, llavors la lírica és més agradable que el càlcul).
Intransitivitat: quan donats tres elements, si el primer es relaciona amb el segon i est amb ell tercer, el primer no es relaciona amb el tercer. (Exemple: Si Jacob és pare de Josep i Josep és pare d'Efraïm, Jacob no és pare d'Efraïm).
Connexitat: quan per qualsevol parell d'elements del camp, succeeix o que el primer es relaciona amb el segon o que el segon es relaciona amb el primer. (Exemple: O Anna està a la dreta de Raül o Raül està a la dreta d'Anna).
Certes propietats s'associen. Així succeeix amb l'equivalència i l'ordre. Si una relació és reflexiva, simètrica i transitiva és també una relació d'equivalència. La relació d'identitat és un cas de relació d'equivalència. Els elements del camp d'una relació (com d'un conjunt, d'una classe) poden estar ordenats. Per a qualsevol classe d'ordenació, les propietats comunes són la transitivitat i la simetria.
Augustus De Morgan, Charles S. Peirce i Ernst Schröder (1841-1902) són autors destacats en el desenvolupament de l'àlgebra o de la lògica de relacions.
Una funció és una classe de relació.
