Fractals, geometria dels

Fractal: el conjunt de Mandelbrot.

(deriva del llatí «fractus»: trencat, irregular, i suggereix també ho fraccional i fragmentari)

Designa una entitat geomètrica creada pel matemàtic Benoit B. Mandelbrot, que consta de fragments geomètrics d'orientació i grandària variable encara que d'aspecte semblant, de manera que, si ho ampliem (o reduïm), encara que canviï l'escala, es mostra com una sèrie repetitiva de nivells similars. És a dir, que posseeix la propietat de l'autosimilitud o sibisemejanza, obtinguda per un procés d'iteració repetida d'unes formes que es van autoreplicant.

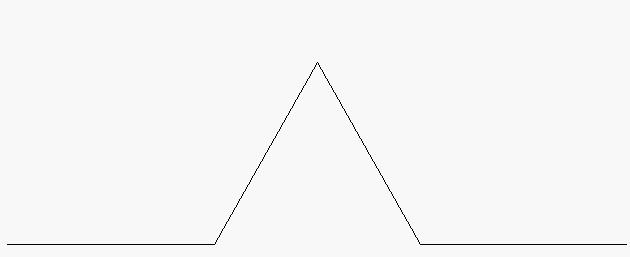
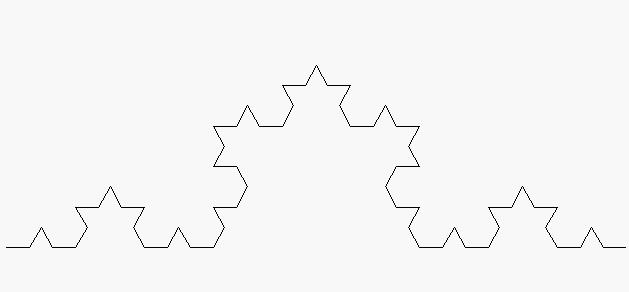
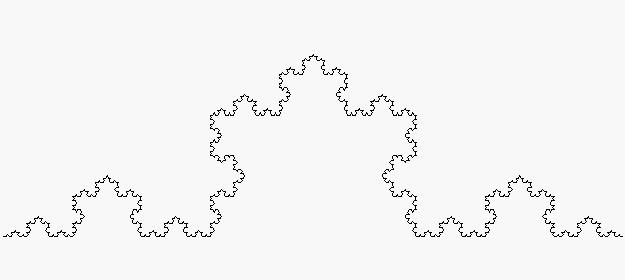
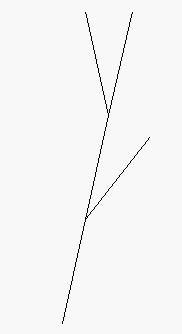
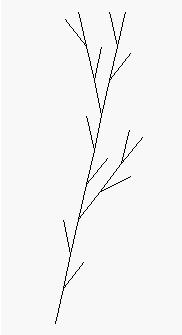
La geometria fractal té els seus antecedents en l'obra d'alguns matemàtics del segle XIX, tals com Koch, Cantor, Peano, Hilbert, Sierpinski, i uns altres, que ja van estudiar des de les singularitats de corbes no derivables, fins a la formació recursiva de determinades formes geomètriques, com la corba de Peano (veure imatge), la corba d'Hilbert (veure imatge), la corba d'H. von Koch (coneguda com a «floc de neu», veure imatge), la «catifa» de Sierpinski, o l'«esponja» de Menger (entitats matemàtiques que tenen una àrea finita però un perímetre infinit, o una superfície infinita però un volum nul). Però es deu a Mandelbrot el ple desenvolupament d'aquesta nova geometria que s'aplica a l'estudi de nombrosos fenòmens relacionats amb la teoria del caos, tals com l'estudi de: formes naturals no descriptibles mitjançant geometries convencionals, la forma de les línies costaneres, la formació de muntanyes, la forma dels núvols, dels polímers, les circumvolucions cerebrals, la formació i ramificació de les estructures pulmonars, la ramificació d'arbres i arbustos (veure imatge), l'estudi de patrons meteorològics, i els processos de la morfogènesi biològica. A més, aplicant la geometria fractal, s'han creat algorismes de compressió i de generació d'imatges de gran aplicació en informàtica, en vídeo i en cinematografia.

L'aplicació de la geometria fractal permet entendre els sistemes complexos de la naturalesa, que semblen preservar i recapitular l'aspecte dels detalls en escales cada vegada més fines, la qual cosa suggereix principis o patrons de creixement i de forma regits per lleis matemàtiques similars i, per tant, aplicables a múltiples àmbits d'investigació. Aquesta geometria, com la teoria de les catàstrofes de René Thom, ha revitalitzat aspectes qualitatius en la matemàtica, i s'incardina en un procés de renovació holística de la ciència.

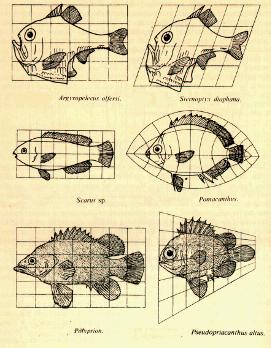
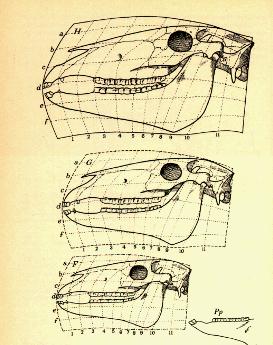
Segons Mandelbrot, la geometria fractal, com la teoria de la relativitat o la mecànica quàntica, descobreix una interdependència entre el subjecte i l'objecte en el procés de mesurament, ja que l'objecte mesurat depèn de les escales utilitzades per l'observador. Amb això, la noció de magnitud es relativitza i es posa en funció de l'escala o perspectiva de l'observador. Així, en lloc de les magnituds quantitatives, Mandelbrot proposa una mesura qualitativa de dimensions fractals que expressa el grau de complexitat relativa d'un objecte. A més, posa en dubte la creença segons la qual les formes complexes han d'estar generades per processos complexos, ja que els fractals, malgrat la seva gran complexitat, poden generar-se per iteracions successives de formes simples. Es poden obtenir formes fractals molt complexes repetint una transformació geomètrica simple, i petits canvis en els paràmetres d'aquesta transformació, provoquen canvis globals. Això permet abordar des d'una perspectiva nova (encara que ja entrevista per d'Arcy Thomson a principis de segle (veure imatges) l'estudi de la morfogènesi, i permet aplicar la geometria fractal a l'estudi de la transmissió genètica. Però, com ja hem dit anteriorment, l'àmbit d'aplicació de la teoria dels fractals és molt ampli: des de l'economia, fins a la cosmologia; des de la física de fluids, fins a la cartografia. D'aquesta manera, la geometria fractal apareix com una teoria descriptiva general del canvi que és independent del substrat que ho origina.

Encara que en una estructura fractal domina l'autosemejanza, no hi ha pròpiament autoidentitat. Es verifiquen canvis: cada part d'una figura fractal és una imatge replicada de la totalitat, una espècie de microcosmos que replica a la seva escala el macrocosmos al qual pertany, però amb variacions. Aquesta estructura holística s'assembla també a la dels hologrames que, en dividir-se o tallar-se, reprodueixen la figura completa. Amb això, semblen recuperar-se alguns antics models holístics del món però, lluny de la mera especulació, es funden en sòlides investigacions que ofereixen un sistema descriptiu de gran potència i permeten esbossar noves metodologies d'investigació de la complexitat de la naturalesa.

Veure imatges d'exemple ↓