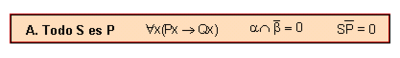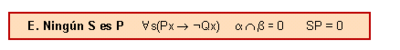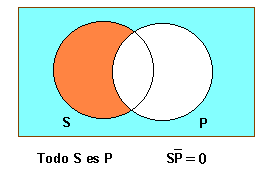Diferència entre revisions de la pàgina «Diagrames de Venn»
De Wikisofia
m (Text de reemplaçament - "rayado" a "ratllat") |
|||
| Línia 1: | Línia 1: | ||
| − | {{ConcepteWiki}} | + | {{ConcepteWiki}} Mètode gràfic, ideat pel lògic anglès [[Autor:Venn,_John|John Venn]], que permet representar les relacions de classe existents entre els [[Terme|termes]] dels [[Enunciat_categòric|enunciats categòrics]] i solucionar, d'una manera fàcil i intuïtiu, la [[Validesa|validesa]] dels raonaments [[Sil·logística|sil·logístics]]. |
| − | Mètode gràfic, ideat pel lògic anglès [[Autor:Venn,_John|John Venn]], que permet representar les relacions de classe existents entre els [[ | ||
| − | ===Diagrames=== | + | === Diagrames === |
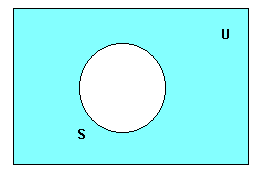
| − | Un rectangle representa l'[[ | + | Un rectangle representa l'[[Univers_del_discurs|univers del discurs]], O, i un cercle a l'interior de l'univers representa una [[Classe_(lògica)|classe]] o un [[Terme|terme]], que s'afirma en aquest univers, determinant dues zones: la zona interior del cercle, en què estan, o poden estar, els elements d'aquesta classe, i la zona exterior al cercle on estan els elements de la classe complemento : |
| − | [[File:3682-1.png|400px| | + | [[File:3682-1.png|center|400px|3682-1.png]] |
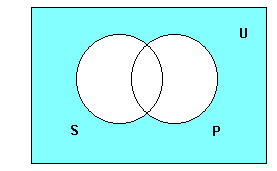
| − | Un cercle pot estar simplement dibuixat, o afirmat, ratllat o acolorit, això és ''buit ''d'elements, i altres pot intersecar amb un altre cercle, representant d'aquesta manera un enunciat categòric. En aquest cas, s'assignen lletres majúscules S,P,Q,, ..., a cada cercle; les lletres representen [[ | + | Un cercle pot estar simplement dibuixat, o afirmat, ratllat o acolorit, això és ''buit ''d'elements, i altres pot intersecar amb un altre cercle, representant d'aquesta manera un enunciat categòric. En aquest cas, s'assignen lletres majúscules S,P,Q,, ..., a cada cercle; les lletres representen [[Classe_(lògica)|classes]] o termes: |
| − | |||
| − | |||
| − | |||
| + | [[File:3682-2.png|center|400px|3682-2.png]] | ||
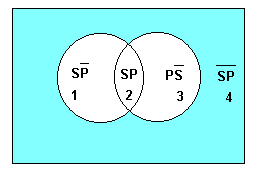
La representació de dos cercles intersecantes determina la creació de quatre tipus de zones: | La representació de dos cercles intersecantes determina la creació de quatre tipus de zones: | ||
| − | [[File:3682-3.png|400px| | + | [[File:3682-3.png|center|400px|3682-3.png]] |
La '''zona 1''': on estan els elements de S, però no de P. | La '''zona 1''': on estan els elements de S, però no de P. | ||
| Línia 24: | Línia 21: | ||
La '''zona 3''': on estan els elements de P, però no de S. | La '''zona 3''': on estan els elements de P, però no de S. | ||
| − | La''' zona 4''': on estan els elements que no són ni S ni P. | + | La'''zona 4''': on estan els elements que no són ni S ni P. |
___________________________________________________________________________________ | ___________________________________________________________________________________ | ||
| − | ===Representació gràfica d'enunciats categòrics=== | + | === Representació gràfica d'enunciats categòrics === |
| − | [[File:3682-4.png|400px| | + | [[File:3682-4.png|center|400px|3682-4.png]] |
L'enunciat categòric universal afirmatiu, de tipus [[A|A]], per exemple, «Tots els homes són iguals», es representa mitjançant la intersecció de dos cercles, buidant (rayando o acolorint) la zona corresponent a . | L'enunciat categòric universal afirmatiu, de tipus [[A|A]], per exemple, «Tots els homes són iguals», es representa mitjançant la intersecció de dos cercles, buidant (rayando o acolorint) la zona corresponent a . | ||
| − | [[File:3682-5.png|400px| | + | [[File:3682-5.png|center|400px|3682-5.png]] |
on l'enunciat «Tots els homes són iguals» ha d'interpretar-se com «Res que sigui home no és igual», o «No hi ha S que no sigui P». | on l'enunciat «Tots els homes són iguals» ha d'interpretar-se com «Res que sigui home no és igual», o «No hi ha S que no sigui P». | ||
| − | |||
___________________________________________________________________________________ | ___________________________________________________________________________________ | ||
| − | [[File:3682-6.png|400px| | + | [[File:3682-6.png|center|400px|3682-6.png]] |
L'enunciat categòric universal negatiu, de tipus [[I|I]], com per exemple, «Cap home és immortal», es representa buidant (rayando o acolorint) la zona d'intersecció corresponent a SP = 0. | L'enunciat categòric universal negatiu, de tipus [[I|I]], com per exemple, «Cap home és immortal», es representa buidant (rayando o acolorint) la zona d'intersecció corresponent a SP = 0. | ||
| − | + | [[File:3682-7.png|center|400px|3682-7.png]] | |
| − | [[File:3682-7.png|400px| | ||
on l'enunciat «Cap home és immortal» ha de llegir-se com «Res és home i immortal a un temps», o «No hi ha S i P a un temps». | on l'enunciat «Cap home és immortal» ha de llegir-se com «Res és home i immortal a un temps», o «No hi ha S i P a un temps». | ||
| Línia 52: | Línia 47: | ||
___________________________________________________________________________________ | ___________________________________________________________________________________ | ||
| − | [[File:3682-8.png|400px| | + | [[File:3682-8.png|center|400px|3682-8.png]] |
L'enunciat categòric particular afirmatiu, de tipus [[I|I]], per exemple, «Alguns homes són savis», es representa afirmant que la zona d'intersecció de S i P no és buida: que existeix, almenys, un element de la mateixa, que dibuixem marcant amb una X. | L'enunciat categòric particular afirmatiu, de tipus [[I|I]], per exemple, «Alguns homes són savis», es representa afirmant que la zona d'intersecció de S i P no és buida: que existeix, almenys, un element de la mateixa, que dibuixem marcant amb una X. | ||
| − | [[File:3682-9.png|400px| | + | [[File:3682-9.png|center|400px|3682-9.png]] |
de manera que l'enunciat «Alguns homes són savis» ha de llegir-se com «Hi ha homes que són savis», o «Hi ha S i P a un temps». | de manera que l'enunciat «Alguns homes són savis» ha de llegir-se com «Hi ha homes que són savis», o «Hi ha S i P a un temps». | ||
| Línia 62: | Línia 57: | ||
___________________________________________________________________________________ | ___________________________________________________________________________________ | ||
| − | [[File:3682-10.jpg|center]] | + | [[File:3682-10.jpg|center|3682-10.jpg]] |
L'enunciat categòric particular negatiu, de tipus [[O|O]], per exemple, «Alguns homes no són lliures», es representa afirmant que no és buida la zona formada pels elements que són S i no P a un temps: que en tal zona existeix almenys un element de la mateixa, que dibuixem marcant amb una X. | L'enunciat categòric particular negatiu, de tipus [[O|O]], per exemple, «Alguns homes no són lliures», es representa afirmant que no és buida la zona formada pels elements que són S i no P a un temps: que en tal zona existeix almenys un element de la mateixa, que dibuixem marcant amb una X. | ||
| − | [[File:3682-11.png|400px| | + | [[File:3682-11.png|center|400px|3682-11.png]] |
| − | de manera que l'enunciat «Alguns homes no són lliures» es llegeix com «Hi ha homes que no són lliures», o « Hi ha S i no P a un temps» | + | de manera que l'enunciat «Alguns homes no són lliures» es llegeix com «Hi ha homes que no són lliures», o « Hi ha S i no P a un temps» |
___________________________________________________________________________________ | ___________________________________________________________________________________ | ||
| Línia 76: | Línia 71: | ||
<math>\alpha \cap \overline{\beta}= 0</math> | <math>\alpha \cap \overline{\beta}= 0</math> | ||
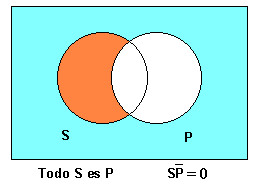
| − | '''Tot S és P ''' | + | '''Tot S és P''' |
| − | [[File:3350-5.png|400px]] | + | [[File:3350-5.png|400px|3350-5.png]] |
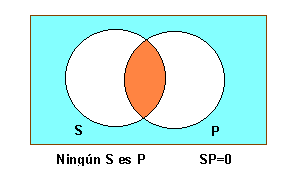
| − | '''Cap S és P ''' | + | '''Cap S és P''' |
<math>\alpha \cap \beta= 0</math> | <math>\alpha \cap \beta= 0</math> | ||
| − | [[File:3350-6.png|400px]] | + | [[File:3350-6.png|400px|3350-6.png]] |
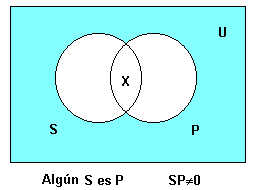
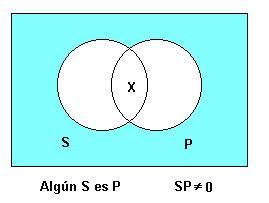
'''Algun S és P''' | '''Algun S és P''' | ||
| Línia 90: | Línia 85: | ||
<math>\alpha \cap \beta \neq 0</math> | <math>\alpha \cap \beta \neq 0</math> | ||
| − | [[File:3350-7.png|400px]] | + | [[File:3350-7.png|400px|3350-7.png]] |
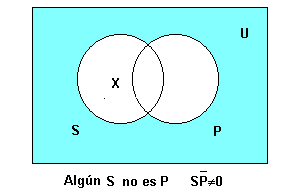
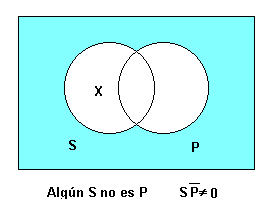
'''Algun S no és P''' | '''Algun S no és P''' | ||
| Línia 96: | Línia 91: | ||
<math>\alpha \cap \overline{\beta} \neq 0</math> | <math>\alpha \cap \overline{\beta} \neq 0</math> | ||
| − | [[File:3350-8.png|400px]] | + | [[File:3350-8.png|400px|3350-8.png]] |
| − | |||
___________________________________________________________________________________ | ___________________________________________________________________________________ | ||
| − | ===Representació gràfica dels sil·logismes=== | + | === Representació gràfica dels sil·logismes === |
En els raonaments sil·logístics els enunciats components són tres, per tant l'univers queda dibuixat de la següent manera: | En els raonaments sil·logístics els enunciats components són tres, per tant l'univers queda dibuixat de la següent manera: | ||
| − | [[File:3682-12.png|400px| | + | [[File:3682-12.png|center|400px|3682-12.png]] |
Els tres cercles corresponents als termes, S, P i M, delimiten vuit zones que representen la seva extensió: quatre zones d'intersecció i quatre zones de no intersecció. Cada enunciat del sil·logisme, ja sigui premissa o conclusió, afirma alguna cosa sobre algunes d'aquestes zones. | Els tres cercles corresponents als termes, S, P i M, delimiten vuit zones que representen la seva extensió: quatre zones d'intersecció i quatre zones de no intersecció. Cada enunciat del sil·logisme, ja sigui premissa o conclusió, afirma alguna cosa sobre algunes d'aquestes zones. | ||
| Línia 118: | Línia 112: | ||
:Els remugants són herbívors | :Els remugants són herbívors | ||
| − | : | + | ::Les girafes són remugants |
| − | :Les girafes són remugants | ||
:_____________________________ | :_____________________________ | ||
| − | : | + | ::Les girafes són herbívores |
| − | :Les girafes són herbívores | ||
| − | |||
| − | Per comprovar | + | Per comprovar la seva [[Validesa|validesa]]: |
(1) dibuixar successivament ambdues premisses sobre el mateix univers: | (1) dibuixar successivament ambdues premisses sobre el mateix univers: | ||
| − | [[File:3682-13.png|400px| | + | [[File:3682-13.png|center|400px|3682-13.png]] |
| − | de manera que constitueixin un sol | + | de manera que constitueixin un sol diagrama : |
| − | [[File:3682-14.png|400px| | + | [[File:3682-14.png|center|400px|3682-14.png]] |
(2) Comprovar que la conclusió queda ja dibuixada en el diagrames de les premisses: | (2) Comprovar que la conclusió queda ja dibuixada en el diagrames de les premisses: | ||
| − | [[File:3682-15.png|400px| | + | [[File:3682-15.png|center|400px|3682-15.png]] |
[[Recurs:Exemples_lògics:_diagrames_de_Venn|Veure exemples]]. | [[Recurs:Exemples_lògics:_diagrames_de_Venn|Veure exemples]]. | ||
| Línia 147: | Línia 138: | ||
{{Etiqueta | {{Etiqueta | ||
|Etiqueta=Lògica | |Etiqueta=Lògica | ||
| − | }} | + | }} {{InfoWiki}} |
| − | {{InfoWiki}} | ||
Revisió del 17:46, 14 ago 2015
Mètode gràfic, ideat pel lògic anglès John Venn, que permet representar les relacions de classe existents entre els termes dels enunciats categòrics i solucionar, d'una manera fàcil i intuïtiu, la validesa dels raonaments sil·logístics.
Diagrames
Un rectangle representa l'univers del discurs, O, i un cercle a l'interior de l'univers representa una classe o un terme, que s'afirma en aquest univers, determinant dues zones: la zona interior del cercle, en què estan, o poden estar, els elements d'aquesta classe, i la zona exterior al cercle on estan els elements de la classe complemento :
Un cercle pot estar simplement dibuixat, o afirmat, ratllat o acolorit, això és buit d'elements, i altres pot intersecar amb un altre cercle, representant d'aquesta manera un enunciat categòric. En aquest cas, s'assignen lletres majúscules S,P,Q,, ..., a cada cercle; les lletres representen classes o termes:
La representació de dos cercles intersecantes determina la creació de quatre tipus de zones:
La zona 1: on estan els elements de S, però no de P.
La zona 2: on estan els elements de S i P.
La zona 3: on estan els elements de P, però no de S.
Lazona 4: on estan els elements que no són ni S ni P.
___________________________________________________________________________________
Representació gràfica d'enunciats categòrics
L'enunciat categòric universal afirmatiu, de tipus A, per exemple, «Tots els homes són iguals», es representa mitjançant la intersecció de dos cercles, buidant (rayando o acolorint) la zona corresponent a .
on l'enunciat «Tots els homes són iguals» ha d'interpretar-se com «Res que sigui home no és igual», o «No hi ha S que no sigui P».
___________________________________________________________________________________
L'enunciat categòric universal negatiu, de tipus I, com per exemple, «Cap home és immortal», es representa buidant (rayando o acolorint) la zona d'intersecció corresponent a SP = 0.
on l'enunciat «Cap home és immortal» ha de llegir-se com «Res és home i immortal a un temps», o «No hi ha S i P a un temps».
___________________________________________________________________________________
L'enunciat categòric particular afirmatiu, de tipus I, per exemple, «Alguns homes són savis», es representa afirmant que la zona d'intersecció de S i P no és buida: que existeix, almenys, un element de la mateixa, que dibuixem marcant amb una X.
de manera que l'enunciat «Alguns homes són savis» ha de llegir-se com «Hi ha homes que són savis», o «Hi ha S i P a un temps».
___________________________________________________________________________________
L'enunciat categòric particular negatiu, de tipus O, per exemple, «Alguns homes no són lliures», es representa afirmant que no és buida la zona formada pels elements que són S i no P a un temps: que en tal zona existeix almenys un element de la mateixa, que dibuixem marcant amb una X.
de manera que l'enunciat «Alguns homes no són lliures» es llegeix com «Hi ha homes que no són lliures», o « Hi ha S i no P a un temps»
___________________________________________________________________________________
Exemples
[math]\displaystyle{ \alpha \cap \overline{\beta}= 0 }[/math]
Tot S és P
Cap S és P
[math]\displaystyle{ \alpha \cap \beta= 0 }[/math]
Algun S és P
[math]\displaystyle{ \alpha \cap \beta \neq 0 }[/math]
Algun S no és P
[math]\displaystyle{ \alpha \cap \overline{\beta} \neq 0 }[/math]
___________________________________________________________________________________
Representació gràfica dels sil·logismes
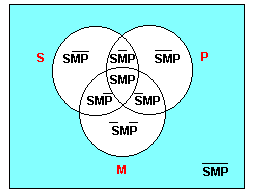
En els raonaments sil·logístics els enunciats components són tres, per tant l'univers queda dibuixat de la següent manera:
Els tres cercles corresponents als termes, S, P i M, delimiten vuit zones que representen la seva extensió: quatre zones d'intersecció i quatre zones de no intersecció. Cada enunciat del sil·logisme, ja sigui premissa o conclusió, afirma alguna cosa sobre algunes d'aquestes zones.
Es considera vàlid aquell sil·logisme en què ocorre que, en dibuixar les premisses, queda ja dibuixada la conclusió.
___________________________________________________________________________________
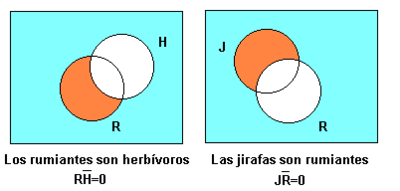
Exemple:
Sigui el següent sil·logisme:
- Els remugants són herbívors
- Les girafes són remugants
- _____________________________
- Les girafes són herbívores
Per comprovar la seva validesa:
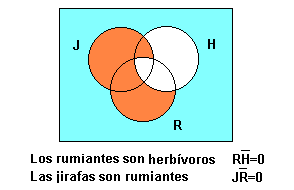
(1) dibuixar successivament ambdues premisses sobre el mateix univers:
de manera que constitueixin un sol diagrama :
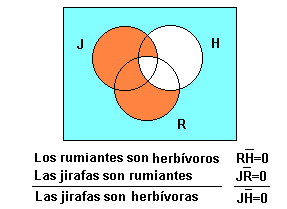
(2) Comprovar que la conclusió queda ja dibuixada en el diagrames de les premisses:
___________________________________________________________________________________
De la mateixa manera, amb igual mètode és possible comprovar gràficament la invalidesa d'alguns raonaments sil·logístics. Veure exemple.