A
De Wikisofia
Símbol que s'aplica als enunciats que corresponen a les denominades proposicions categòriques universals afirmatives de la lògica clàssica.
Són enunciats del tipus «Tots els S són P», en els quals S és el terme subjecte i P el terme predicat, amb la quantitat universal i la qualitat afirmativa. Moltes són les maneres de formular aquesta classe d'enunciats:
Tot el que és S és P
Tot S és P
El S és P
Cada S és P
Allò que és un S és un P
Si alguna cosa és S, és P
Si S, P
Si alguna cosa és S llavors és P
Només si és P és S
Res que no sigui P és S
Res és S si no és P
No hi ha cap S que no sigui P
No hi ha S que no sigui P
Els enunciats tipus A juntament amb els del tipus I (particulars afirmatius) formen el grup dels enunciats afirmatius (del llatí affirmo provenen precisament els símbols A i I corresponents). Els enunciats tipus A se dibuixen de la següent manera, amb els diagrames de Venn:
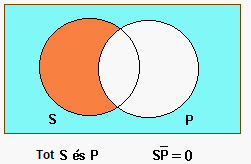
on la regió [math]\displaystyle{ S\overline{P} }[/math] és buida, ja que s'afirma que tot S pertany a P.
Segons la interpretació de la lògica tradicional, se suposa que el terme subjecte denota, raó per la qual ha d'existir algun terme S a la zona SP (mentre que no hi ha informació sobre si n'hi ha també a la zona [math]\displaystyle{ \overline{S}P }[/math]
Segons la interpretació que la lògica moderna fa d'aquests enunciats, no ha d'entendre's que «Tot S és P» implica que existeix algun S, raó per la qual la forma correcta d'entendre aquests enunciats és «Si existeix algun S, llavors és P».
Las tradicionals oposicions aristotèliques s'expressen como:
⋀ x ( F x → G x ) ↔ ¬ ⋁ x ( F x ∧ ¬ G x )
⋀ x ( F x → ¬ G x ) ↔ ¬ ⋁ x ( F x ∧ G x )
⋁ x ( F x ∧ G x ) ↔ ¬ ⋀ x ( F x → ¬ G x )
⋁ x ( F x ∧ ¬ G x ) ↔ ¬ ⋀ x ( F x → G x )