Hipòtesi, confirmació d'

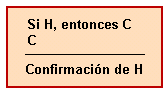
Segons el mètode hipotètic-deductiu, és la recol·lecció d'observacions, experiments i contrastacions amb la intenció de buscar raons per admetre una hipòtesi. Segueix el següent esquema d'argumentació:

On H és la hipòtesi que es vol confirmar i C una conseqüència que es dedueix de la mateixa. Si C es compleix realment, s'obté com a conclusió del raonament la confirmació de H. Es tracta d'un argument no deductiu (anomenat en lògica fal·làcia de l'afirmació del conseqüent), que només té valor inductiu: el que es conclou és que, provada la veritat de C, H té major probabilitat. L'aspecte deductiu radica només en què C s'ha deduït lògicament de H.

veure exemple ↓

Si H [math]\displaystyle{ d=1/2gt^2]\rightarrow{}C[d }[/math] en [math]\displaystyle{ 2t = 19,6m] }[/math]

efectivament C

__________________

Es confirma H

Si g és la constant de gravitació (9,80m/s), t el temps i d la distància recorreguda, llavors per la hipòtesi de Galileu, [math]\displaystyle{ d=(\frac{1}{2})gt^2 }[/math], i del fet que un objecte, partint del repòs, ha estat caient durant 2 segons, podem inferir vàlidament l'enunciat veritable que ha recorregut 19'6 m. Si mesurem en un cas concret d'un cos en caiguda lliure que aquesta és la distància recorreguda, la hipòtesi de Galileu guanya confirmació addicional amb aquesta i altres comprovacions similars.

______________________________________________________________

W. Gustason, Reasoning from Evidence, Macmillan, Nova York 1994, p. 214.

Recurs:Exemple de W. Gustason sobre inferència

i veg. text).

Una teoria de la confirmació és una teoria de la inferència inductiva. Segueixen tres exemples de inferència inductiva:

L'esquema simple abans esmentat, es completa amb el següent (on P és la predicció, SA els supòsits auxiliars, CI les condicions inicials i H la hipòtesi :

S'ha produït un error en crear la miniatura: Fitxer inexistent

Com tots dos esquemes constitueixen en realitat un argument que no és deductivament vàlid, es proposen altres models de raonament amb major força inductiva:

1) Plantejament de W. Gustason

S'ha produït un error en crear la miniatura: Fitxer inexistent

On, en la línia 3, Pr(H/I) significa la probabilitat preferent d'una hipòtesi H que es funda en les evidències I (proves), abans de provar com a veritable la predicció P, i aquesta probabilitat és major, en la línia 4, que la de qualsevol altra hipòtesi amb la qual entre en competència (Cf. W. Gustason, Reasoning from Evidence, Macmillan, Nova York 1994, p. 219).

2) Plantejament de Ronald N. Giere

S'ha produït un error en crear la miniatura: Fitxer inexistent

La línia 3 és un Modus tollens; la línia 4 s'obté per les lleis de De Morgan; la línia 5 és una premissa que se suposa veritable. (Cf. R.N. Giere, Understanding Scientific Reasoning, Holt, Rinehart and Winston, Nova York 1979, p. 96).