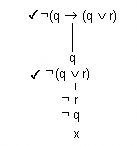Diferència entre revisions de la pàgina «Arbres lògics, càlcul de»
De Wikisofia
(Es crea la pàgina amb «{{ConcepteWiki}} Càlcul lògic introduït per I.B. Beth (1955), i adaptat per altres autors, com J. Hintikka i R. Smull...».) |
m (Text de reemplaçament - "2307S" a "2307Scat") |
||
| (6 revisions intermèdies per 2 usuaris que no es mostren) | |||
| Línia 1: | Línia 1: | ||
{{ConcepteWiki}} | {{ConcepteWiki}} | ||
| − | [[càlcul lògic|Càlcul]] lògic introduït per I.B. Beth (1955), i adaptat per altres autors, com [[Autor:Hintikka, Jaakko|J. Hintikka]] i R. Smullyan, com a procediment per decidir si una [[fórmula|fórmula]] és vàlida o no. Pertany als sistemes formals sintàctics (que no recorren al significat o [[interpretació|interpretació]] dels seus símbols), i es basa fonamentalment en la propietat | + | [[càlcul lògic|Càlcul]] lògic introduït per I.B. Beth (1955), i adaptat per altres autors, com [[Autor:Hintikka, Jaakko|J. Hintikka]] i R. Smullyan, com a procediment per a decidir si una [[fórmula|fórmula]] és vàlida o no. Pertany als sistemes formals sintàctics (que no recorren al significat o [[interpretació|interpretació]] dels seus símbols), i es basa fonamentalment en la propietat d'[[inconsistència|inconsistència]] entre enunciats i que un raonament invàlid posseeix almenys un [[contraexemple|contraexemple]]. |
Segons aquest càlcul, la seqüència <math>A_1, A_2, A_n</math>, per tant <math>B</math> <br> | Segons aquest càlcul, la seqüència <math>A_1, A_2, A_n</math>, per tant <math>B</math> <br> | ||
| Línia 6: | Línia 6: | ||
<math>A_1, A_2, A_n</math>, per tant <math>no-B</math>, és inconsistent. | <math>A_1, A_2, A_n</math>, per tant <math>no-B</math>, és inconsistent. | ||
| − | Si es vol construir una [[deducció|deducció]], s'escriu (com no-B) la ''negació de la conclusió''; si el que es vol provar és si una única fórmula és [[validesa|vàlida]], o | + | Si es vol construir una [[deducció|deducció]], s'escriu (com no-B) la ''negació de la conclusió''; si el que es vol provar és si una única fórmula és [[validesa|vàlida]], o tautològica, s'escriu (com no-B) la seva ''negació''. |
S'estructura a manera d'arbre invertit, i d'aquí el seu nom, format per un conjunt finit de fórmules; les que componen el conjunt de [[premisses|premisses]] i la negació de la conclusió constitueixen el tronc; les derivacions d'aquestes segons les regles del mètode d'arbres formen les branques. | S'estructura a manera d'arbre invertit, i d'aquí el seu nom, format per un conjunt finit de fórmules; les que componen el conjunt de [[premisses|premisses]] i la negació de la conclusió constitueixen el tronc; les derivacions d'aquestes segons les regles del mètode d'arbres formen les branques. | ||
| − | S'aplica una regla quan es transforma una fórmula donada en els seus components, segons determina la definició de la regla. Quan no hi ha més fórmules | + | S'aplica una regla quan es transforma una fórmula donada en els seus components, segons determina la definició de la regla. Quan no hi ha més fórmules per a descompondre, s'acaba la ramificació de l'arbre. Llavors, apareixen dues possibilitats: |
:1) que una(s) branca(s) (o totes) estigui(n) ''tancada(s)'': una branca està tancada quan en la seva ramificació (en la seva línia) ha aparegut una [[contradicció|contradicció]]; cosa que s'indica amb una X. | :1) que una(s) branca(s) (o totes) estigui(n) ''tancada(s)'': una branca està tancada quan en la seva ramificació (en la seva línia) ha aparegut una [[contradicció|contradicció]]; cosa que s'indica amb una X. | ||
| Línia 17: | Línia 17: | ||
| − | Una fórmula queda demostrada (sigui una fórmula [[tautologia| | + | Una fórmula queda demostrada (sigui una fórmula [[tautologia|tautològica]], sigui la conclusió d'una [[deducció|deducció]]) quan de l'arbre pot tancar (marcant amb X) totes les seves branques. El procediment demostra que la negació de la fórmula que es vol deduir no és consistent, per a qualsevol valor, amb la resta de premisses, o que la negació de la fórmula el valor de la qual s'analitza és [[contradictoris|contradictòria]] per a qualsevol valor assignat a les seves lletres d'enunciat. |
Un arbre es compon, per tant, de les [[premisses|premisses]] propostes i de la [[negació|negació]] de la conclusió suposada; de diferents aplicacions de les regles de transformació i de les expressions lògiques finals, tancades (amb X) o obertes. | Un arbre es compon, per tant, de les [[premisses|premisses]] propostes i de la [[negació|negació]] de la conclusió suposada; de diferents aplicacions de les regles de transformació i de les expressions lògiques finals, tancades (amb X) o obertes. | ||
| Línia 32: | Línia 32: | ||
que pot ser la formalització del següent raonament: | que pot ser la formalització del següent raonament: | ||
| − | «Si Anna canta i | + | «Si Anna canta i Raül no toca el piano, Anna desafina. Però Raül només |
toca el piano si Berta no està present. Anna canta i Berta està present. | toca el piano si Berta no està present. Anna canta i Berta està present. | ||
| Línia 48: | Línia 48: | ||
El seu arbre lògic és: | El seu arbre lògic és: | ||
| − | [[File: | + | [[File:2307Scat.png|400px]] |
Per tant, si <math>¬[q\rightarrow{(q\vee t)}]</math> és una contradicció, <math>q\rightarrow{(q\vee t)}</math> és una tautologia. | Per tant, si <math>¬[q\rightarrow{(q\vee t)}]</math> és una contradicció, <math>q\rightarrow{(q\vee t)}</math> és una tautologia. | ||
| Línia 62: | Línia 62: | ||
| − | + | Vegeu [[lògica|arbres lògics]], en [[lògica|lògica d'enunciats]] i [[lògica|lògica de predicats]]. | |
Revisió de 14:20, 22 oct 2018
Càlcul lògic introduït per I.B. Beth (1955), i adaptat per altres autors, com J. Hintikka i R. Smullyan, com a procediment per a decidir si una fórmula és vàlida o no. Pertany als sistemes formals sintàctics (que no recorren al significat o interpretació dels seus símbols), i es basa fonamentalment en la propietat d'inconsistència entre enunciats i que un raonament invàlid posseeix almenys un contraexemple.
Segons aquest càlcul, la seqüència [math]\displaystyle{ A_1, A_2, A_n }[/math], per tant [math]\displaystyle{ B }[/math]
és un raonament vàlid si i només si el seu contraexemple,
[math]\displaystyle{ A_1, A_2, A_n }[/math], per tant [math]\displaystyle{ no-B }[/math], és inconsistent.
Si es vol construir una deducció, s'escriu (com no-B) la negació de la conclusió; si el que es vol provar és si una única fórmula és vàlida, o tautològica, s'escriu (com no-B) la seva negació.
S'estructura a manera d'arbre invertit, i d'aquí el seu nom, format per un conjunt finit de fórmules; les que componen el conjunt de premisses i la negació de la conclusió constitueixen el tronc; les derivacions d'aquestes segons les regles del mètode d'arbres formen les branques.
S'aplica una regla quan es transforma una fórmula donada en els seus components, segons determina la definició de la regla. Quan no hi ha més fórmules per a descompondre, s'acaba la ramificació de l'arbre. Llavors, apareixen dues possibilitats:
- 1) que una(s) branca(s) (o totes) estigui(n) tancada(s): una branca està tancada quan en la seva ramificació (en la seva línia) ha aparegut una contradicció; cosa que s'indica amb una X.
- 2) que alguna branca (o totes) quedi oberta: una branca està oberta quan en ella no apareix cap contradicció. Això indica que existeix alguna assignació de valors que satisfà (fa veritable a) la conclusió.
Una fórmula queda demostrada (sigui una fórmula tautològica, sigui la conclusió d'una deducció) quan de l'arbre pot tancar (marcant amb X) totes les seves branques. El procediment demostra que la negació de la fórmula que es vol deduir no és consistent, per a qualsevol valor, amb la resta de premisses, o que la negació de la fórmula el valor de la qual s'analitza és contradictòria per a qualsevol valor assignat a les seves lletres d'enunciat.
Un arbre es compon, per tant, de les premisses propostes i de la negació de la conclusió suposada; de diferents aplicacions de les regles de transformació i de les expressions lògiques finals, tancades (amb X) o obertes.
Les regles del mètode d'arbres, per la lògica d'enunciats, són les següents:
Exemples:
1. Derivar s del següent conjunt de fórmules
que pot ser la formalització del següent raonament:
«Si Anna canta i Raül no toca el piano, Anna desafina. Però Raül només
toca el piano si Berta no està present. Anna canta i Berta està present.
Per tant, Anna desafina»
2. Per a les tautologies,
Exemple 1
Sigui la tautologia [math]\displaystyle{ q\rightarrow{(q\vee t)} }[/math]
El seu arbre lògic és:
Per tant, si [math]\displaystyle{ ¬[q\rightarrow{(q\vee t)}] }[/math] és una contradicció, [math]\displaystyle{ q\rightarrow{(q\vee t)} }[/math] és una tautologia.
Exemple 2
Tot el que agrada o és il·legal, o immoral o engreixa. Prendre's un gelat és agradable. Prendre's un gelat no és il·legal ni immoral. Per tant, prendre's un gelat engreixa.
La seva formalització és:
Vegeu arbres lògics, en lògica d'enunciats i lògica de predicats.