Zenó d'Elea

(Ζήνων ὁ Ἐλεάτης)

Filòsof grec, nascut a Elea, ciutat jonia del sud d'Itàlia, prop de l'actual Salern, probablement entre el 490 i el 480 a. de C. Deixeble de Parmènides, i segons el text platònic el seu «favorit», sent aquest ja ancià i tenint ell uns quaranta anys, li va acompanyar a Atenes durant les Grans Panateneas (veure cita). Ha passat a la història del pensament com el defensor de les idees de Parmènides contra els atacs dels pluralistes i el divulgador de la seva filosofia, adduint arguments coneguts com paradoxes de Zenó, que, des del punt de vista lògic, suposen la prova d'una hipòtesi per reducció a l'absurd; aquesta és la raó per la qual, en ocasions, és considerat iniciador de la dialèctica. Amb aquests arguments «refuta a els qui afirmen la multiplicitat» (tant si és infinitament divisible com si no) i defensa, per aquesta raó, que «tot és un» (veure cita).

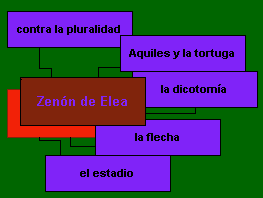
Aquests arguments contra la multiplicitat són pròpiament arguments contra la divisibilidad de l'espai i el temps, i els noms amb que es coneixen els principals (se li atribueixen uns quaranta logoi, o arguments) són: «Aquil·les i la tortuga», la paradoxa de «la dicotomia», «la fletxa», «l'estadi» i la paradoxa de «la pluralitat». Les dues primeres paradoxes argumenten des de l'absurd de suposar que l'espai -una línia o una distància- pugui ser infinitament divisible; les dos següents argumenten des del supòsit, que es manifesta absurd, que temps o espai es componguin d'elements indivisibles; la cinquena i última paradoxa rebutja l'absurd de suposar que temps o espai es componen de quantitats, extenses o inextenses.

Els cinc arguments poden reduir-se a l'esquema següent:

Al llarg de la història s'ha valorat diversament el sentit d'aquestes paradoxes (veure paradoxes de Zenó), i s'ha tendit a creure que les nocions modernes de «límit» i «infinitesimal» poden solucionar les aporías, considerant el problema, no des de la perspectiva de l'espai o del temps com a quantitats contínues o discontínues, sinó des de l'aspecte de la «velocitat» amb la qual es recorren distàncies que poden definir-se com una sèrie de valors convergents al límit.