Diferència entre revisions de la pàgina «Veritat, valors de»
De Wikisofia
m (bot: - </div> Veure enunciat + </div> Vegeu enunciat) |
m (Text de reemplaçament - "veritativos" a "veritatius") |
||
| Línia 1: | Línia 1: | ||
{{ConcepteWiki}} | {{ConcepteWiki}} | ||
| − | També anomenats «valors | + | També anomenats «valors veritatius»: la doble possibilitat de l'[[enunciat|enunciat]] de ser [[veritat|veritable]] o fals. L'enunciat veritable té el valor de veritat, i l'enunciat fals el valor de falsedat. La [[lògica|lògica]] tradicional, que es funda en el [[bivalència, principi de|principi de bivalència]], admet només aquests dos valors. També el valor de veritat o falsedat que rep una [[fórmula|fórmula]] lògica en rebre una interpretació. |
La [[lògica|lògica d'enunciats]] es diu [[veritativo-funcional, enunciat|veritativo-funcional]] perquè el valor de veritat dels seus enunciats depèn de les [[connectors, connectives|connectives]] definides com una [[funció|funció]] de veritat; aquestes funcions es defineixen mitjançant [[lògica|taules de veritat]] | La [[lògica|lògica d'enunciats]] es diu [[veritativo-funcional, enunciat|veritativo-funcional]] perquè el valor de veritat dels seus enunciats depèn de les [[connectors, connectives|connectives]] definides com una [[funció|funció]] de veritat; aquestes funcions es defineixen mitjançant [[lògica|taules de veritat]] | ||
Revisió del 11:30, 14 juny 2018
També anomenats «valors veritatius»: la doble possibilitat de l'enunciat de ser veritable o fals. L'enunciat veritable té el valor de veritat, i l'enunciat fals el valor de falsedat. La lògica tradicional, que es funda en el principi de bivalència, admet només aquests dos valors. També el valor de veritat o falsedat que rep una fórmula lògica en rebre una interpretació.
La lògica d'enunciats es diu veritativo-funcional perquè el valor de veritat dels seus enunciats depèn de les connectives definides com una funció de veritat; aquestes funcions es defineixen mitjançant taules de veritat
(veg. exemple 1 ↓)
i
(veg. exemple 2 ↓)
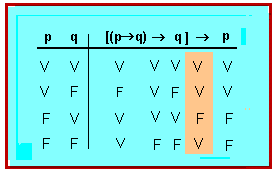
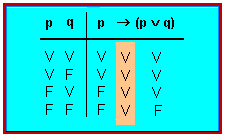
Les taules de veritat lògiques posen de manifest com les connectives són símbols veritativo-funcionals, o símbols que designen una funció veritativa entre un enunciat compost i els valors de veritat:
Així, per a l'enunciat:
[math]\displaystyle{ p \rightarrow{q} (p \vee q) }[/math]
la taula de veritat és
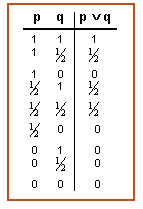
Altres lògiques admeten més de dos valors; per exemple, la lògica trivalent de Lukasiewicz, que admet veritable, fals i indeterminat.
i
Vegeu enunciat veritativo-funcional.
Vegeu termes relacionats.