Diferència entre revisions de la pàgina «Les lleis de Kepler»
De Wikisofia
(Es crea la pàgina amb «{{RecursWiki |Tipus=Extractes d'obres }} {{RecursoEnlace |Enllaç= }} {{Multimèdia |Upload Type= |File= |Embed= }} {{RecursBase |Nom=Les lleis de Kepler...».) |
|||
| Línia 34: | Línia 34: | ||
| − | {{Ref|Ref=Cf. M. Zeilik, ''Astronomy. The evolving universe'', John Wiley & Sons, | + | {{Ref|Ref=Cf. M. Zeilik, ''Astronomy. The evolving universe'', John Wiley & Sons, Nueva York 1988, 5ª ed., p. 47-48.|Cita=true}} |
{{Propietat | {{Propietat | ||
|Propi=No | |Propi=No | ||
Revisió del 22:56, 31 ago 2015
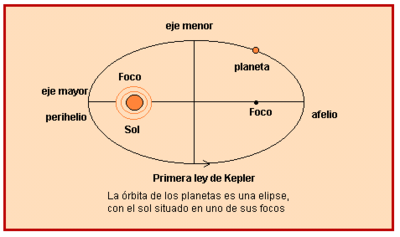
Plantilla:RecursoEnlace Plantilla:Multimèdia Primera llei: llei de l'el·lipse (1609). L'òrbita de cada planeta és una el·lipse, amb el sol en un dels seus focus.
(Conseqüència: la distància del planeta al sol varia al llarg de l'òrbita).
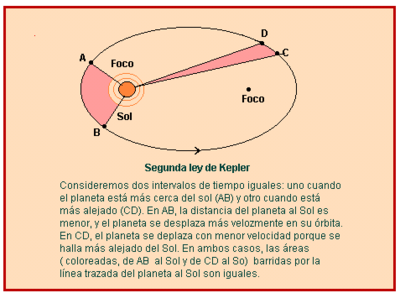
Segona llei: llei de les àrees (1609). Una línia traçada des d'un planeta al sol escombra àrees iguals en temps iguals.
(Conseqüència: la velocitat de desplaçament no és uniforme: a major distància del sol, menor velocitat).
Tercera llei: llei harmònica (1619). El quadrat del període d'un planeta és directament proporcional al cub de la seva distància mitjana al sol. Algebraicament, [math]\displaystyle{ P^2 = ca^3 }[/math], on P és el període orbital, a la distància mitjana al sol i k una constant.
(Conseqüència: a major òrbita solar, menor velocitat de desplaçament del planeta).
| Cf. M. Zeilik, Astronomy. The evolving universe, John Wiley & Sons, Nueva York 1988, 5ª ed., p. 47-48. |
Original en castellà
Primera ley: ley de la elipse (1609). La órbita de cada planeta es una elipse, con el sol en uno de sus focos.
(Consecuencia: la distancia del planeta al sol varía a lo largo de la órbita).

Segunda ley: ley de las áreas (1609). Una línea trazada desde un planeta al sol barre áreas iguales en tiempos iguales.
(Consecuencia: la velocidad de desplazamiento no es uniforme: a mayor distancia del sol, menor velocidad).

Tercera ley: ley armónica (1619). El cuadrado del período de un planeta es directamente proporcional al cubo de su distancia media al sol. Algebraicamente, [math]\displaystyle{ P^2 = ka^3 }[/math], donde P es el período orbital, a la distancia media al sol y k una constante.
(Consecuencia: a mayor órbita solar, menor velocidad de desplazamiento del planeta).