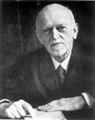Diferència entre revisions de la pàgina «Hilbert, David»
De Wikisofia
m (bot: - és, freturosos de + és, mancats de) |
|||
| (2 revisions intermèdies per un altre usuari que no es mostra) | |||
| Línia 4: | Línia 4: | ||
|Cognom=Hilbert | |Cognom=Hilbert | ||
}} | }} | ||
| − | + | Matemàtic i lògic alemany, nascut a Königsberg –la ciutat en què va néixer i va viure [[Autor:Kant, Immanuel|Kant]]–, professor a Gotinga. El seu nom va unit, sobretot, al de [[formalisme|formalisme]] i al de [[matemàtiques, filosofia de les|metamatemática]], ciència que ell funda i que pot entendre's com a «teoria de la demostració» o estudi dels sistemes matemàtics formalitzats, és a dir, mancats de contingut significatiu. Durant els anys 1920-1930, es va dedicar a desenvolupar un programa de formalització del raonament matemàtic, amb l'esperança de provar sobretot la [[consistència|consistència]] de l'aritmètica elemental i la teoria de conjunts, esperança esvaïda, més tard, pel [[incompletesa, teorema de la|teorema de Gödel]], respecte a una teoria aritmètica elemental. | |
| − | |||
| − | |||
| − | |||
| − | Matemàtic i lògic alemany, nascut a Königsberg –la ciutat en què va néixer i va viure [[Autor:Kant, Immanuel|Kant]]–, professor | ||
En ''Fonaments de geometria'' (1899), ofereix una axiomatització de la geometria i a ell es deuen també els primers estudis sobre les propietats formals dels [[sistema axiomàtic|sistemes axiomàtics]]. | En ''Fonaments de geometria'' (1899), ofereix una axiomatització de la geometria i a ell es deuen també els primers estudis sobre les propietats formals dels [[sistema axiomàtic|sistemes axiomàtics]]. | ||
En expressió de J. Dieudonné, Hilbert «ha ensenyat als matemàtics a pensar axiomàticament». Entre les seves obres destaquen: ''Fonaments de geometria'' (1899) i ''Elements de lògica teòrica'' (1928). | En expressió de J. Dieudonné, Hilbert «ha ensenyat als matemàtics a pensar axiomàticament». Entre les seves obres destaquen: ''Fonaments de geometria'' (1899) i ''Elements de lògica teòrica'' (1928). | ||
| + | |||
| + | <center><gallery> | ||
| + | File:hilbert3.gif | ||
| + | File:hilbert4.gif| | ||
| + | File:hilbert5.gif | ||
| + | File:hilbert6.gif | ||
| + | </gallery></center> | ||
| + | |||
{{ImatgePrincipal | {{ImatgePrincipal | ||
|Imatge=hilbert1.gif | |Imatge=hilbert1.gif | ||
Revisió de 18:44, 17 oct 2018
Avís: El títol a mostrar «David Hilbert» sobreescriu l'anterior títol a mostrar «Hilbert, David».
Matemàtic i lògic alemany, nascut a Königsberg –la ciutat en què va néixer i va viure Kant–, professor a Gotinga. El seu nom va unit, sobretot, al de formalisme i al de metamatemática, ciència que ell funda i que pot entendre's com a «teoria de la demostració» o estudi dels sistemes matemàtics formalitzats, és a dir, mancats de contingut significatiu. Durant els anys 1920-1930, es va dedicar a desenvolupar un programa de formalització del raonament matemàtic, amb l'esperança de provar sobretot la consistència de l'aritmètica elemental i la teoria de conjunts, esperança esvaïda, més tard, pel teorema de Gödel, respecte a una teoria aritmètica elemental.
En Fonaments de geometria (1899), ofereix una axiomatització de la geometria i a ell es deuen també els primers estudis sobre les propietats formals dels sistemes axiomàtics.
En expressió de J. Dieudonné, Hilbert «ha ensenyat als matemàtics a pensar axiomàticament». Entre les seves obres destaquen: Fonaments de geometria (1899) i Elements de lògica teòrica (1928).