Diferència entre revisions de la pàgina «Quadrat d'oposicions»
De Wikisofia
m (bot: - per determinar les + per a determinar les) |
|||
| (Hi ha 6 revisions intermèdies del mateix usuari que no es mostren) | |||
| Línia 1: | Línia 1: | ||
{{Exemple}} | {{Exemple}} | ||
| − | Diagrama mnemotècnic, d'origen medieval, que permet determinar les relacions i les [[inferència immediata|inferències immediates]] que s'estableixen entre [[enunciat categòric|enunciats categòrics]]. | + | Diagrama mnemotècnic, d'origen medieval, que permet determinar les relacions i les [[inferència immediata|inferències immediates]] que s'estableixen entre [[enunciat categòric|enunciats categòrics]]. Anomenant «[[A|A]]» als enunciats universals afirmatius, «[[I|I]]», als universals negatius, «[[I|I]]», als particulars afirmatius, i «[[O|O]]» als particulars negatius, es pot traçar el següent diagrama: |
| − | [[File: | + | <center>[[File:906catala.jpg|400px]]</center> |
| − | On els [[contraris|contraris]] són A i | + | On els [[contraris|contraris]] són A i E; els [[contradictoris|contradictoris]] A i O, E i I; els [#subcontraris subcontraris] I i O, i on entre A i I, i entre E i O s'estableix una relació de subalternació. |
Això implica que: | Això implica que: | ||
| Línia 16: | Línia 16: | ||
En una subordinació, el subordinat es pot deduir vàlidament del subordinant, però no al revés, de manera que si A és veritable, I també ho és, i si I és veritable, O també ho és ([[Recurs:Lògica: exemple de subordinació|veg. exemple]]). | En una subordinació, el subordinat es pot deduir vàlidament del subordinant, però no al revés, de manera que si A és veritable, I també ho és, i si I és veritable, O també ho és ([[Recurs:Lògica: exemple de subordinació|veg. exemple]]). | ||
| − | Aquest quadre pot utilitzar-se també per a determinar les relacions entre les [[modalitats alètiques|modalitats alètiques]] o enunciats modals i entre [[enunciat deòntic|enunciats deòntics]]. De manera que A, | + | Aquest quadre pot utilitzar-se també per a determinar les relacions entre les [[modalitats alètiques|modalitats alètiques]] o enunciats modals i entre [[enunciat deòntic|enunciats deòntics]]. De manera que A,E,I i O poden interpretar-se de la següent manera: |
| − | A: | + | '''A:''' |
:Tot S és | :Tot S és | ||
| Línia 27: | Línia 27: | ||
:És obligatori fer S | :És obligatori fer S | ||
| − | + | '''E:''' | |
:Tot S és no-P | :Tot S és no-P | ||
| Línia 35: | Línia 35: | ||
:És obligatori fer no-S | :És obligatori fer no-S | ||
| − | + | '''I:''' | |
| − | :Algun S és | + | :Algun S és P : |
| − | P : | ||
:És possible S | :És possible S | ||
: | : | ||
:Està permès fer S (facultatiu) | :Està permès fer S (facultatiu) | ||
| − | O: | + | '''O''': |
:Algun S és no-P | :Algun S és no-P | ||
| Línia 54: | Línia 53: | ||
De manera que, reinterpretant el quadre d'oposicions, tenim: | De manera que, reinterpretant el quadre d'oposicions, tenim: | ||
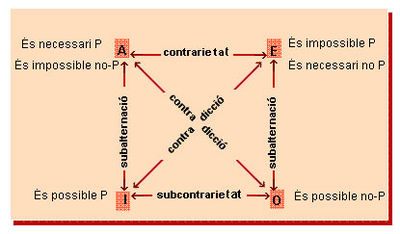
| − | [[File:906B. | + | [[File:906B.jpg|400px|center]] |
| − | '''Són ''enunciats contraris'' (A i | + | '''Són ''enunciats contraris'' (A i E)''': |
Si «tot S és P» és veritable, llavors «cap S és P» és fals | Si «tot S és P» és veritable, llavors «cap S és P» és fals | ||
| Línia 66: | Línia 65: | ||
| − | '''Són enunciats ''contradictoris ''(A i O, | + | '''Són enunciats ''contradictoris ''(A i O, E i I)''': |
Si «tot S és P» és veritable, llavors «algun S no és P» és fals | Si «tot S és P» és veritable, llavors «algun S no és P» és fals | ||
Revisió de 15:06, 17 maig 2018
Diagrama mnemotècnic, d'origen medieval, que permet determinar les relacions i les inferències immediates que s'estableixen entre enunciats categòrics. Anomenant «A» als enunciats universals afirmatius, «I», als universals negatius, «I», als particulars afirmatius, i «O» als particulars negatius, es pot traçar el següent diagrama:
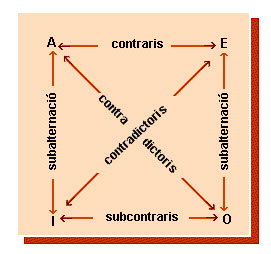
On els contraris són A i E; els contradictoris A i O, E i I; els [#subcontraris subcontraris] I i O, i on entre A i I, i entre E i O s'estableix una relació de subalternació.
Això implica que:
Dos enunciats contraris no poden ser tots dos veritables alhora, però poden ser tots dos falsos (veg. exemple).
Dos enunciats contradictoris no poden ser tots dos veritables ni tots dos falsos; si un és veritable, l'altre és fals, i viceversa (veg. exemple).
Dos enunciats subcontraris no poden ser tots dos falsos alhora, però poden ser tots dos veritables (veg. exemple).
En una subordinació, el subordinat es pot deduir vàlidament del subordinant, però no al revés, de manera que si A és veritable, I també ho és, i si I és veritable, O també ho és (veg. exemple).
Aquest quadre pot utilitzar-se també per a determinar les relacions entre les modalitats alètiques o enunciats modals i entre enunciats deòntics. De manera que A,E,I i O poden interpretar-se de la següent manera:
A:
- Tot S és
P :
- És necessari S
- És obligatori fer S
E:
- Tot S és no-P
- És necessari no-S
- És obligatori fer no-S
I:
- Algun S és P :
- És possible S
- Està permès fer S (facultatiu)
O:
- Algun S és no-P
- És possible no-S
- Està permès fer no-S (facultatiu)
De manera que, reinterpretant el quadre d'oposicions, tenim:
Són enunciats contraris (A i E):
Si «tot S és P» és veritable, llavors «cap S és P» és fals
Si és veritat que «p és necessari», llavors és fals que «és necessari no-p», o que «és impossible p» (veg. exemple).
Si és veritat que «és obligatori fer p», llavors és fals que «és obligatori no fer no-p» (veg. exemple).
Són enunciats contradictoris (A i O, E i I):
Si «tot S és P» és veritable, llavors «algun S no és P» és fals
Si «és necessari p», llavors no «és possible no-p» (veg. exemple).
Si «és obligatori fer p», llavors no «està permès fer no-p» (veg. exemple).
Si «cap S és P» és veritable, llavors «algun S és P» és fals
Si «és necessari no-p», llavors és fals que «és possible p» (veg. exemple).
Si «és obligatori fer no-p», llavors no és veritat que «estigui permès fer p» (veg. exemple).
Són enunciats subcontraris (I i O):
Si «algun S és P» és fals, llavors «algun S no és P» és veritable.
Si «és possible p» és fals, llavors «és possible no-p» és veritable (veg. exemple).
Si és fals que «està permès fer p», llavors és veritat que «està permès fer no-p» (veg. exemple).
Però sempre són possibles ambdues coses:
Que «algun S sigui P» i que «algun S no sigui P» ; que sigui «possible p» i que sigui «possible no-p», i que estigui permitidio «fer p» i estigui permès «fer no-p». Plantilla:Propietat