Diferència entre revisions de la pàgina «Quadre d'oposicions»
De Wikisofia
(permès) |
|||
| (12 revisions intermèdies per 2 usuaris que no es mostren) | |||
| Línia 1: | Línia 1: | ||
{{ConcepteWiki}} | {{ConcepteWiki}} | ||
| − | Diagrama mnemotècnic, d'origen medieval, que permet determinar les relacions i les [[inferència immediata|inferències immediates]] que s'estableixen entre [[enunciat categòric|enunciats categòrics]]. | + | Diagrama mnemotècnic, d'origen medieval, que permet determinar les relacions i les [[inferència immediata|inferències immediates]] que s'estableixen entre [[enunciat categòric|enunciats categòrics]]. Anomenant «[[A|A]]» als enunciats universals afirmatius, «[[I|I]]», als universals negatius, «[[I|I]]», als particulars afirmatius, i «[[O|O]]» als particulars negatius, es pot traçar el següent diagrama: |
| − | [[File: | + | <center>[[File:906catala.jpg|400px]]</center> |
| − | On els [[contraris|contraris]] són A i | + | On els [[contraris|contraris]] són '''A''' i '''E'''; els [[contradictoris|contradictoris]] '''A''' i '''O''', '''E''' i '''I'''; els subcontraris '''I''' i '''O''', i on entre '''A''' i '''I''', i entre '''E''' i '''O''' s'estableix una relació de subalternació. |
| − | Això implica que : | + | Això implica que: |
| − | Dos enunciats contraris no poden ser tots dos veritables alhora, però poden ser tots dos falsos | + | Dos enunciats contraris no poden ser tots dos veritables alhora, però poden ser tots dos falsos. |
| − | + | <div class='mw-collapsible mw-collapsed'> | |
| + | <center>(Veg. exemple ↓)</center> | ||
| + | <div class='mw-collapsible-content'> | ||
| − | + | Si és veritat que «Totes les alumnes aproven» és fals que «Cap alumna aprova», però tots dos enunciats poden ser falsos. | |
| − | + | ([[Recurs:Lògica: exemple d'enunciats contraris|veg. exemple]]). | |
| + | </div></div> | ||
| − | + | Dos enunciats contradictoris no poden ser tots dos veritables ni tots dos falsos; si un és veritable, l'altre és fals, i viceversa. | |
| + | <div class='mw-collapsible mw-collapsed'> | ||
| + | <center>(Veg. exemple ↓)</center> | ||
| + | <div class='mw-collapsible-content'> | ||
| − | A: | + | Dos enunciats contradictoris no poden ser tots dos veritables ni tots dos falsos; si un és veritable, l'altre és fals, i viceversa: |
| + | |||
| + | Si és veritat que «totes les alumnes aproven» és fals que «alguna alumna no aprova»; si aquest últim enunciat és veritable, llavors el primer és fals. | ||
| + | |||
| + | Si és veritat que «cap alumna suspèn», llavors és fals que «alguna alumna suspèn»; si és veritable aquest últim enunciat, és fals l'anterior. | ||
| + | |||
| + | ([[Recurs:Lògica: exemple d'enunciats contradictoris|veg. exemple]]). | ||
| + | </div></div> | ||
| + | |||
| + | |||
| + | Dos enunciats subcontraris no poden ser tots dos falsos alhora, però poden ser tots dos veritables. | ||
| + | |||
| + | <div class='mw-collapsible mw-collapsed'> | ||
| + | <center>(Veg. exemple ↓)</center> | ||
| + | <div class='mw-collapsible-content'> | ||
| + | Si és fals que «alguna alumna suspèn», llavors és veritat que «alguna alumna no suspèn». | ||
| + | |||
| + | Si és veritat que «alguna alumna suspèn», també pot ser veritat que «alguna alumna no suspèn». | ||
| + | |||
| + | ([[Recurs:Lògica: exemple d'enunciats subcontraris|veg. exemple]]). | ||
| + | </div></div> | ||
| + | |||
| + | En una subordinació, el subordinat es pot deduir vàlidament del subordinant, però no al revés, de manera que si A és veritable, I també ho és, i si I és veritable, O també ho és. | ||
| + | |||
| + | <div class='mw-collapsible mw-collapsed'> | ||
| + | <center>(Veg. exemple ↓)</center> | ||
| + | <div class='mw-collapsible-content'> | ||
| + | Si és veritable que «totes les alumnes aproven», és veritable també que «alguna alumna aprova». | ||
| + | |||
| + | Si és veritable que «cap alumna aprova», llavors és veritable que «alguna alumna no aprova». | ||
| + | |||
| + | ([[Recurs:Lògica: exemple de subordinació|veg. exemple]]). | ||
| + | </div></div> | ||
| + | |||
| + | Aquest quadre pot utilitzar-se també per a determinar les relacions entre les [[modalitats alètiques|modalitats alètiques]] o enunciats modals i entre [[enunciat deòntic|enunciats deòntics]]. De manera que A,E,I i O poden interpretar-se de la següent manera: | ||
| + | |||
| + | |||
| + | '''[[A]]:''' | ||
| + | |||
| + | :Tot S és P | ||
| − | |||
| − | |||
:És necessari S | :És necessari S | ||
: | : | ||
:És obligatori fer S | :És obligatori fer S | ||
| − | + | '''[[E]]:''' | |
:Tot S és no-P | :Tot S és no-P | ||
| Línia 35: | Línia 78: | ||
:És obligatori fer no-S | :És obligatori fer no-S | ||
| − | + | '''[[I]]:''' | |
| − | :Algun S és | + | :Algun S és P : |
| − | P : | ||
:És possible S | :És possible S | ||
: | : | ||
:Està permès fer S (facultatiu) | :Està permès fer S (facultatiu) | ||
| − | O: | + | '''[[O]]''': |
:Algun S és no-P | :Algun S és no-P | ||
| Línia 54: | Línia 96: | ||
De manera que, reinterpretant el quadre d'oposicions, tenim: | De manera que, reinterpretant el quadre d'oposicions, tenim: | ||
| − | [[File:906B. | + | <center>[[File:906B.jpg|400px]]</center> |
| + | |||
| + | |||
| + | '''Són ''enunciats contraris'' (A i E)''': | ||
| + | |||
| + | Si «tot S és P» és vertader, llavors «cap S és P» és fals | ||
| + | Si és veritat que «p és necessari», llavors és fals que «és necessari no-p», o que «és impossible p» | ||
| + | <div class='mw-collapsible mw-collapsed'> | ||
| + | <center>(Veg. exemple ↓)</center> | ||
| + | <div class='mw-collapsible-content'> | ||
| − | + | Si és veritat que és necessari que un triangle tingui tres costats, llavors és fals que sigui necessari que un triangle no tingui tres costats, o que és impossible que els tingui. | |
| − | + | ([[Recurs:Lògica: veritat i necessitat|veg. exemple]]). | |
| + | </div></div> | ||
| − | Si és veritat que | + | Si és veritat que «és obligatori fer p», llavors és fals que «és obligatori no fer no-p» |
| − | Si és veritat que «és obligatori | + | <div class='mw-collapsible mw-collapsed'> |
| + | <center>(Veg. exemple ↓)</center> | ||
| + | <div class='mw-collapsible-content'> | ||
| + | Si és veritat que «és obligatori ser solidaris amb els altres», llavors és fals que sigui obligatori no ser-ho, o que estigui permès no ser-ho. | ||
| + | ([[Recurs:Lògica: veritat i obligatorietat|veg. exemple]]). | ||
| + | </div></div> | ||
| − | '''Són enunciats ''contradictoris ''(A i O, | + | '''Són enunciats ''contradictoris '' ''' ('''A''' i '''O''', '''E''' i '''I'''): |
Si «tot S és P» és veritable, llavors «algun S no és P» és fals | Si «tot S és P» és veritable, llavors «algun S no és P» és fals | ||
| − | Si «és necessari p», llavors no «és possible no-p» ( | + | Si «és necessari p», llavors no «és possible no-p» |
| + | <div class='mw-collapsible mw-collapsed'> | ||
| + | <center>(Veg. exemple ↓)</center> | ||
| + | <div class='mw-collapsible-content'> | ||
| − | Si «és obligatori fer p», llavors no «està permès fer no-p» ([[Recurs:Exemple: obligatori i permès| | + | Si és necessari que el plom s'enfonsi, llavors no és possible que no s'enfonsi, o és fals que pugui no enfonsar-se. |
| + | |||
| + | ([[Recurs:Exemple de necessitat i possibilitat|veg. exemple]]). | ||
| + | </div></div> | ||
| + | |||
| + | Si «és obligatori fer p», llavors no «està permès fer no-p» | ||
| + | |||
| + | <div class='mw-collapsible mw-collapsed'> | ||
| + | <center>(Veg. exemple ↓)</center> | ||
| + | <div class='mw-collapsible-content'> | ||
| + | |||
| + | Si és obligatori tornar el robat, no està permès quedar-se amb el robat | ||
| + | |||
| + | ([[Recurs:Exemple: obligatori i permès|veg. exemple]]). | ||
| + | </div></div> | ||
Si «cap S és P» és veritable, llavors «algun S és P» és fals | Si «cap S és P» és veritable, llavors «algun S és P» és fals | ||
| − | Si «és necessari no-p», llavors és fals que «és possible p» ([[Recurs:Exemple: necessari i possible| | + | Si «és necessari no-p», llavors és fals que «és possible p» |
| + | |||
| + | <div class='mw-collapsible mw-collapsed'> | ||
| + | <center>(Veg. exemple ↓)</center> | ||
| + | <div class='mw-collapsible-content'> | ||
| + | |||
| + | Si cal que un cercle no sigui quadrat, llavors no és possible que sigui quadrat | ||
| + | |||
| + | ([[Recurs:Exemple: necessari i possible|veg. exemple]]). | ||
| + | </div></div> | ||
| + | |||
| + | Si «és obligatori fer no-p», llavors no és veritat que «estigui permès fer p» | ||
| − | + | <div class='mw-collapsible mw-collapsed'> | |
| + | <center>(Veg. exemple ↓)</center> | ||
| + | <div class='mw-collapsible-content'> | ||
| − | + | Si és obligatori no defraudar a Hisenda, llavors no és veritat que estigui permès fer-ho. | |
| − | + | ([[Recurs:Exemple lògic|veg. exemple]]). | |
| + | </div></div> | ||
| − | + | '''Són enunciats ''subcontraris'' ''' ('''I''' i '''O''') | |
| − | Si és fals que «està permès fer p», llavors és veritat que «està permès fer no-p» ([[Recurs:Exemple: fals i | + | Si «algun S és P» és fals, llavors «algun S no és P» és vertader. |
| + | |||
| + | Si «és possible p» és fals, llavors «és possible no-p» és vertader | ||
| + | |||
| + | <div class='mw-collapsible mw-collapsed'> | ||
| + | <center>(Veg. exemple ↓)</center> | ||
| + | <div class='mw-collapsible-content'> | ||
| + | |||
| + | Si és fals que el ferro pugui surar en l'aigua, llavors és veritat que és possible que s'enfonsi. | ||
| + | |||
| + | ([[Recurs:Exemple: fals i veritable|veg. exemple]]) | ||
| + | </div></div>. | ||
| + | |||
| + | Si és fals que «està permès fer p», llavors és veritat que «està permès fer no-p» | ||
| + | |||
| + | <div class='mw-collapsible mw-collapsed'> | ||
| + | <center>(Veg. exemple ↓)</center> | ||
| + | <div class='mw-collapsible-content'> | ||
| + | |||
| + | Si és fals que estigui permès circular per l'esquerra en una calçada de doble direcció, llavors és veritat que està permès fer-ho per la dreta. | ||
| + | |||
| + | ([[Recurs:Exemple: fals i vertader (2)|veg. exemple]]). | ||
| + | </div></div> | ||
Però sempre són possibles ambdues coses: | Però sempre són possibles ambdues coses: | ||
| − | Que «algun S sigui P» i que «algun S no sigui P»; que sigui «possible p» i que sigui «possible no-p», i que estigui permès «fer p» i estigui permès «fer no-p». | + | Que «algun S sigui P» i que «algun S no sigui P» ; que sigui «possible p» i que sigui «possible no-p», i que estigui permès «fer p» i estigui permès «fer no-p». |
| + | |||
| + | {{InfoWiki}} | ||
{{Etiqueta | {{Etiqueta | ||
Revisió de 23:04, 28 set 2018
Diagrama mnemotècnic, d'origen medieval, que permet determinar les relacions i les inferències immediates que s'estableixen entre enunciats categòrics. Anomenant «A» als enunciats universals afirmatius, «I», als universals negatius, «I», als particulars afirmatius, i «O» als particulars negatius, es pot traçar el següent diagrama:
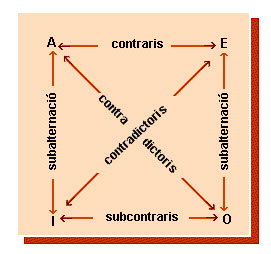
On els contraris són A i E; els contradictoris A i O, E i I; els subcontraris I i O, i on entre A i I, i entre E i O s'estableix una relació de subalternació.
Això implica que:
Dos enunciats contraris no poden ser tots dos veritables alhora, però poden ser tots dos falsos.
Si és veritat que «Totes les alumnes aproven» és fals que «Cap alumna aprova», però tots dos enunciats poden ser falsos.
(veg. exemple).
Dos enunciats contradictoris no poden ser tots dos veritables ni tots dos falsos; si un és veritable, l'altre és fals, i viceversa.
Dos enunciats contradictoris no poden ser tots dos veritables ni tots dos falsos; si un és veritable, l'altre és fals, i viceversa:
Si és veritat que «totes les alumnes aproven» és fals que «alguna alumna no aprova»; si aquest últim enunciat és veritable, llavors el primer és fals.
Si és veritat que «cap alumna suspèn», llavors és fals que «alguna alumna suspèn»; si és veritable aquest últim enunciat, és fals l'anterior.
(veg. exemple).
Dos enunciats subcontraris no poden ser tots dos falsos alhora, però poden ser tots dos veritables.
Si és fals que «alguna alumna suspèn», llavors és veritat que «alguna alumna no suspèn».
Si és veritat que «alguna alumna suspèn», també pot ser veritat que «alguna alumna no suspèn».
(veg. exemple).
En una subordinació, el subordinat es pot deduir vàlidament del subordinant, però no al revés, de manera que si A és veritable, I també ho és, i si I és veritable, O també ho és.
Si és veritable que «totes les alumnes aproven», és veritable també que «alguna alumna aprova».
Si és veritable que «cap alumna aprova», llavors és veritable que «alguna alumna no aprova».
(veg. exemple).
Aquest quadre pot utilitzar-se també per a determinar les relacions entre les modalitats alètiques o enunciats modals i entre enunciats deòntics. De manera que A,E,I i O poden interpretar-se de la següent manera:
A:
- Tot S és P
- És necessari S
- És obligatori fer S
E:
- Tot S és no-P
- És necessari no-S
- És obligatori fer no-S
I:
- Algun S és P :
- És possible S
- Està permès fer S (facultatiu)
O:
- Algun S és no-P
- És possible no-S
- Està permès fer no-S (facultatiu)
De manera que, reinterpretant el quadre d'oposicions, tenim:
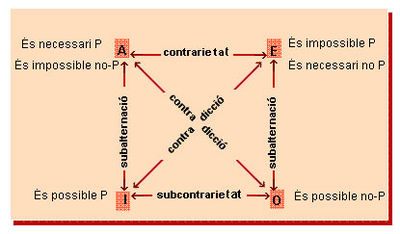
Són enunciats contraris (A i E):
Si «tot S és P» és vertader, llavors «cap S és P» és fals
Si és veritat que «p és necessari», llavors és fals que «és necessari no-p», o que «és impossible p»
Si és veritat que és necessari que un triangle tingui tres costats, llavors és fals que sigui necessari que un triangle no tingui tres costats, o que és impossible que els tingui.
(veg. exemple).
Si és veritat que «és obligatori fer p», llavors és fals que «és obligatori no fer no-p»
Si és veritat que «és obligatori ser solidaris amb els altres», llavors és fals que sigui obligatori no ser-ho, o que estigui permès no ser-ho. (veg. exemple).
Són enunciats contradictoris (A i O, E i I):
Si «tot S és P» és veritable, llavors «algun S no és P» és fals
Si «és necessari p», llavors no «és possible no-p»
Si és necessari que el plom s'enfonsi, llavors no és possible que no s'enfonsi, o és fals que pugui no enfonsar-se.
(veg. exemple).
Si «és obligatori fer p», llavors no «està permès fer no-p»
Si és obligatori tornar el robat, no està permès quedar-se amb el robat
(veg. exemple).
Si «cap S és P» és veritable, llavors «algun S és P» és fals
Si «és necessari no-p», llavors és fals que «és possible p»
Si cal que un cercle no sigui quadrat, llavors no és possible que sigui quadrat
(veg. exemple).
Si «és obligatori fer no-p», llavors no és veritat que «estigui permès fer p»
Si és obligatori no defraudar a Hisenda, llavors no és veritat que estigui permès fer-ho.
(veg. exemple).
Són enunciats subcontraris (I i O)
Si «algun S és P» és fals, llavors «algun S no és P» és vertader.
Si «és possible p» és fals, llavors «és possible no-p» és vertader
Si és fals que el ferro pugui surar en l'aigua, llavors és veritat que és possible que s'enfonsi.
.
Si és fals que «està permès fer p», llavors és veritat que «està permès fer no-p»
Si és fals que estigui permès circular per l'esquerra en una calçada de doble direcció, llavors és veritat que està permès fer-ho per la dreta.
(veg. exemple).
Però sempre són possibles ambdues coses:
Que «algun S sigui P» i que «algun S no sigui P» ; que sigui «possible p» i que sigui «possible no-p», i que estigui permès «fer p» i estigui permès «fer no-p».