Diferència entre revisions de la pàgina «E»
De Wikisofia
(Es crea la pàgina amb «{{ConcepteWiki}} Símbol tradicional que s'aplica als enunciats que corresponen a les denominades proposicions categòriques...».) |
|||
| (Hi ha 4 revisions intermèdies del mateix usuari que no es mostren) | |||
| Línia 2: | Línia 2: | ||
Símbol tradicional que s'aplica als [[enunciat|enunciats]] que corresponen a les denominades [[proposició categòrica|proposicions categòriques]] universals negatives de la [[lògica|lògica]] clàssica. Són enunciats del tipus «Cap S és P», en els quals S és el terme [[subjecte |subjecte]] i P el terme [[predicat|predicat]], amb la [[quantitat|quantitat]] universal i la [[qualitat|qualitat]] negativa. Moltes són les maneres de formular aquesta classe d'enunciats: | Símbol tradicional que s'aplica als [[enunciat|enunciats]] que corresponen a les denominades [[proposició categòrica|proposicions categòriques]] universals negatives de la [[lògica|lògica]] clàssica. Són enunciats del tipus «Cap S és P», en els quals S és el terme [[subjecte |subjecte]] i P el terme [[predicat|predicat]], amb la [[quantitat|quantitat]] universal i la [[qualitat|qualitat]] negativa. Moltes són les maneres de formular aquesta classe d'enunciats: | ||
| − | :Res que sigui S és | + | :Res que sigui S és P |
| − | + | ||
:Res que sigui P és S | :Res que sigui P és S | ||
| − | + | ||
| − | :El que és S no és | + | :El que és S no és P |
| − | + | ||
:El que és P no és S | :El que és P no és S | ||
| + | |||
| + | :Les coses S no són coses P | ||
: | : | ||
| − | + | :Si alguna cosa és S llavors no és P | |
| − | + | ||
| − | :Si alguna cosa és S llavors no és | ||
| − | |||
:Allò que és un S és un no P | :Allò que és un S és un no P | ||
| − | + | ||
| − | :Si alguna cosa és S, no és | + | :Si alguna cosa és S, no és P |
| − | + | ||
:Si P, no és S | :Si P, no és S | ||
: | : | ||
| − | :Res és S tret que no sigui | + | :Res és S tret que no sigui P |
| − | + | ||
| − | :No s'és S tret que no se sigui | + | :No s'és S tret que no se sigui P |
| − | + | ||
:Només si és no P és S | :Només si és no P és S | ||
: | : | ||
| Línia 29: | Línia 29: | ||
| − | + | Els enunciats tipus '''E''' juntament amb els del tipus [[O|'''O''']] (particulars negatius) formen el grup dels enunciats negatius (del llatí ''nego'' provenen precisament els símbols '''E''' i '''O''' corresponents). Els enunciats tipus '''E''' es dibuixen de la següent manera, amb els [[diagrames de Venn|diagrames de Venn]]: | |
| − | [[Image:3682- | + | <center>[[Image:3682-7cat.png|400px]]</center> |
| Línia 40: | Línia 40: | ||
no poden estar buides, perquè els termes corresponents han de tenir [[denotació|denotació]]. Mentre que en la lògica actual, segons la interpretació booleana, les proposicions universals manquen de càrrega existencial, raó per la qual tot enunciat de Tipus I s'interpreta com «Si una cosa és S, llavors no és P», sense suposar que existeixin elements que siguin S o P. | no poden estar buides, perquè els termes corresponents han de tenir [[denotació|denotació]]. Mentre que en la lògica actual, segons la interpretació booleana, les proposicions universals manquen de càrrega existencial, raó per la qual tot enunciat de Tipus I s'interpreta com «Si una cosa és S, llavors no és P», sense suposar que existeixin elements que siguin S o P. | ||
| + | En la lògica de predicats es simbolitza així: | ||
| + | |||
| + | <center><math>\forall x(Fx\rightarrow \neg Gx)</math></center> | ||
{{Etiqueta | {{Etiqueta | ||
Revisió de 22:03, 28 set 2018
Símbol tradicional que s'aplica als enunciats que corresponen a les denominades proposicions categòriques universals negatives de la lògica clàssica. Són enunciats del tipus «Cap S és P», en els quals S és el terme subjecte i P el terme predicat, amb la quantitat universal i la qualitat negativa. Moltes són les maneres de formular aquesta classe d'enunciats:
- Res que sigui S és P
- Res que sigui P és S
- El que és S no és P
- El que és P no és S
- Les coses S no són coses P
- Si alguna cosa és S llavors no és P
- Allò que és un S és un no P
- Si alguna cosa és S, no és P
- Si P, no és S
- Res és S tret que no sigui P
- No s'és S tret que no se sigui P
- Només si és no P és S
- Res és P si és S
Els enunciats tipus E juntament amb els del tipus O (particulars negatius) formen el grup dels enunciats negatius (del llatí nego provenen precisament els símbols E i O corresponents). Els enunciats tipus E es dibuixen de la següent manera, amb els diagrames de Venn:
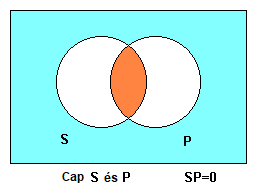
On la regió SP està buida, ja que s'afirma que cap S és alhora P.
En la lògica clàssica se suposa que les zones [math]\displaystyle{ S\overline{P} i \overline{S}P }[/math] no poden estar buides, perquè els termes corresponents han de tenir denotació. Mentre que en la lògica actual, segons la interpretació booleana, les proposicions universals manquen de càrrega existencial, raó per la qual tot enunciat de Tipus I s'interpreta com «Si una cosa és S, llavors no és P», sense suposar que existeixin elements que siguin S o P.
En la lògica de predicats es simbolitza així: