Diferència entre revisions de la pàgina «Argument invàlid»
De Wikisofia
(Es crea la pàgina amb «{{ConcepteWiki}} Aquell que, pel seu forma, admet premisses veritables i conclusió falsa; això és, admet un contraexemple <...».) |
m (Text de reemplaçament - "File:i" a "File:e") |
||
| Línia 47: | Línia 47: | ||
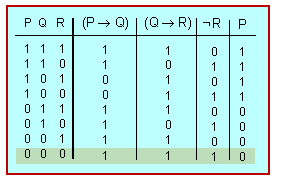
la taula de veritat prova que l'enunciat P és independent de la resta d'enunciats: | la taula de veritat prova que l'enunciat P és independent de la resta d'enunciats: | ||
| − | <center>[[File: | + | <center>[[File:e3491-6.gif]]</center> |
Revisió del 15:40, 25 abr 2015
Aquell que, pel seu forma, admet premisses veritables i conclusió falsa; això és, admet un contraexemple
La següent forma lògica és invàlida :
- Tots els M són P
- Alguns S no són M
- __________________
- Alguns S no són P
Exemple:
- Tots els músics són persones sensibles
- Alguns savis no són músics
- ________________________________________
- Alguns savis no són persones sensibles
Perquè, encara que en aquest cas tant les premisses com la conclusió són veritables, admet contraexemples:
Contraexemple:
- Totes les paraules esdrúixoles s'accentuen
- «Anís» i «patatús» no són paraules esdrúixoles
- ________________________________
- «Anís» i «patatús» no s'accentuen
On les premisses són veritables i la conclusió falsa.
Un argument és invàlid quan la interpretació que fa veritable al conjunt de premisses fa falsa a la conclusió.