Reducció a l'absurd

(del llatí reductio ad absurdum)

Raonament que es basa a demostrar que un conjunt d'afirmacions format per les premisses i la negació de la seva conclusió porta a una contradicció (veg. exemple). Equival a raonar de la següent manera: si el fet de suposar veritable ¬A (no-A) ens porta a una contradicció, llavors A és necessàriament veritable i ¬A necessàriament falsa. Rep també el nom de prova indirecta. De vegades, la reducció a l'absurd només prova que un conjunt de premisses és inconsistent.

Amplia Veg. exemple →

1. Déu és omnipotent.

2. Déu és omniscient.

3. Si Déu és omniscient, Déu pot pensar en tot el que pot ser pensat.

4. Si Déu és omnipotent, Déu pot crear tot el que pot ser pensat.

5. Si Déu és omnipotent, tot el que pot crear el pot també destruir.

6. És possible pensar en una entitat indestructible (aquella precisament que posseeix la propietat de no poder ser destruïda).

_________________________________________________________________

Per tant,

7. Déu pot pensar en tot el que pot ser pensat.

8. En concret, si una entitat indestructible pot ser pensada, Déu pot pensar-la.

9. Déu pot pensar en una entitat indestructible

10. Tot el que Déu pot pensar pot també crear-ho.

11. Si Déu pot pensar en una entitat indestructible, també pot crear una entitat indestructible.

12. Déu pot crear una entitat indestructible.

13. Però tot el que Déu pot crear també pot destruir-ho.

14. En concret, si Déu pot crear una entitat indestructible, llavors Déu pot destruir una entitat indestructible.

15. Déu pot destruir una entitat indestructible

(Però, per definició Déu no pot destruir una entitat indestructible. La conclusió [15] és una contradicció. L'argument és una «reducció a l'absurd» que prova que les premisses 1-6 són inconsistents entre si).

_____________________________________________________________

Pres de W. Neblet, Sherlock's Logic, University Press of America, Lanham-Nova York-Londres 1985, p. 127-128 trad. catal.: La lògica de Sherlock Holmes, La Magrana, Barcelona 1989, p. 125-126).

Històricament, l'ús de raonaments indirectes és normal en geometria; les paradoxes de Zenó han estat contemplades també com a raonaments per reducció a l'absurd.

---

L'esquema lògic d'una reducció a l'absurd és el següent:

[math]\displaystyle{ p\\ .\\ .\\ .\\ q\wedge \neg q\\ }[/math] ____________ [math]\displaystyle{ \neg p }[/math]

Això vol dir que si suposem p i finalment arribem a una contradicció com [math]\displaystyle{ q\wedge \neg q }[/math], llavors hem de concloure la negació de la suposició p, per tant [math]\displaystyle{ \neg p }[/math]

---

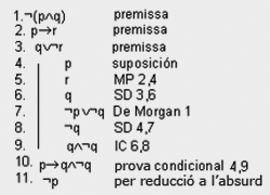
Suposem que es vol demostrar que «Raül no és magnànim» a partir de les premisses:

1. No és possible que Raül sigui magnànim i sever al mateix temps.

2. Si Raül és magnànim, perdona.

3. O Raül és sever o no perdona.

Veg. Apagoge.

Veg. exemple.