Metàfora de la línia (Plató)

Plató

Famós text de Plató que apareix al final del llibre VI de la República (509d-511i) en el qual s'exposa les relacions entre el món sensible i el món de les idees, i assenyala els diversos graus de coneixement, alhora que suggereix el camí i la missió de la dialèctica. És, doncs, un text en el qual es tracta de l'autèntic coneixement filosòfic, del paper de les hipòtesis i de les articulacions entre els diferents nivells ontològics i epistemològics ([#linea veure el text de la metàfora de la línia] ). La continuació d'aquest text és el celebérrimo text del mite de la caverna, que es desenvolupa en el llibre VII de la mateixa obra.

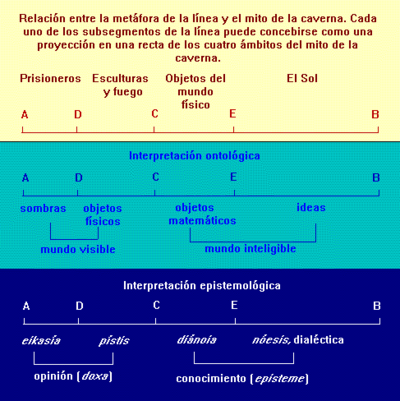
En la metàfora de la línia, Plató proposa que tracem una línia AB i que la dividim en parts desiguals pel punt C, d'aquesta forma obtenim dues subsegmentos: el AC i el CB, sent el primer d'ells més curt que el segon. Tot seguit Plató proposa que considerem el segment més curt com si es tractés d'una imatge o còpia del segment CB i, per tant, més imperfecta (de la mateixa manera que una còpia és inferior a l'original, o que una ombra o un reflex tenen una existència depenent de l'objecte del qual són ombra o reflex), per aquest motiu la representi amb una longitud menor. Posteriorment, assigna a cadascun dels segments la representació de diferents graus de la realitat i de diferents graus del coneixement. D'aquesta manera, ens introdueix en les seves tesis d'una gradació de la realitat en la qual cal considerar diferents graus d'imitació o representació de les idees, així com diferents graus i camins de coneixement. Al seu torn, diu, dividim cadascun d'aquests dos segments mitjançant els punts D i I, seguint la mateixa proporció. De manera que:

AD/DC = CE/EB i, en general, com a AC/CB.

Així obtindrem una línia dividida en 4 segments tal com:

des d'una perspectiva ontològica:

       món sensible                  món intel·ligible

          /      \                               /                \

   ombres  obj. físics           ens matemàtics   idees

A_______D__________C______________I_____________________B

  eikasia    pístis            dianoia noesis       dialèctica

          \     /                                \                  /

     opinió (doxa)              coneixement (episteme)

des d'una perspectiva epistemològica: Punt de vista ontològic

El segment major CB representa, des del punt de vista ontològic, el món intel·ligible.

El segment menor AC representa, el món sensible,

El segment AC se subdivideix en AD i DC, segons la proporció AD/DC=AC/CB, indicant amb això que AD és la imatge de DC, com a AC l'era de CB. D'aquesta manera Plató, des del punt de vista ontològic, situa en el subsegmento inferior AD les ombres i les imatges dels objectes físics reals que estan representats per DC.

Al seu torn, el segment CB també se subdivideix segons la mateixa proporció, de manera que CE representa, des d'un punt de vista ontològic, els ens matemàtics.

El segment EB representa els primers principis, les idees o formes

Tots els segments estan relacionats entre si, i respecte del segmento EB, per la relació «ser imatge de», o «ser representació de».

Punt de vista epistemològic

El segment major CB representa, epistemològicament, el coneixement veritable o episteme (ἐπιστήμη).

El segment menor AC representa la doxa (δόχα) o opinió.

El segment AC se subdivideix en AD i DC, segons la proporció AD/DC=AC/CB, indicant amb això que AD és la imatge de DC, com a AC l'era de CB. D'aquesta manera Plató, des de la perspectiva epistemològica AD representa la creença o pístis (πίστις), i DC la imaginació o eikasia (εἰχασία).

Al seu torn, el segment CB també se subdivideix segons la mateixa proporció, de manera que CE representa, des d'un punt de vista epistemològic, el pensament discursiu o dianoia (διάνοια).

El segment EB representa la raó intuïtiva o noesis (νόεσις) que es desenvolupa dialècticament.

Tots els segments estan relacionats entre si, i respecte del segmento EB, per la relació «ser imatge de», o «ser representació de».

L'aspecte més interessant d'aquesta metàfora no estreba tant en la relació general entre AC i CB (món sensible i món intel·ligible), que Plató desenvolupa de manera més completa en altres textos (com en el mite de la caverna, per exemple), sinó en la relació establerta entre DC i CE, d'una banda, i la relació entre CE i EB, per una altra. En aquestes relacions es posa de manifest l'admissió per part de Plató dels ens matemàtics (als quals, segons Aristòtil, tanta importància donava Plató (veg. text) situats en CE, que es valen dels objectes físics com si aquests fossin imatges d'aquells i, al seu torn, són com a imatges de les autèntiques idees (EB), ocupant un lloc intermedi entre els objectes de la realitat física i el món de les idees. L'existència d'aquests ens és la que permetria a Plató donar un fonament a les matemàtiques i evitar el problema suscitat per l'afirmació de l'existència de diversos cercles, triangles i, en general, la iteració.

Com explicar la possibilitat d'interseccions entre cercles, triangles, iteracions repetides del «mateix» nombre, etc., si solament hi hagués una única idea de circumferència, de triangle, de nombre tres, etc.? Per a solucionar aquest problema, Plató situa en CE els ens matemàtics, còpies perfectes de les idees, però plurals i no idèntiques a elles, que actuarien com a intermediaris entre les veritables idees i la realitat sensible. D'una banda ja són objecte del coneixement científic (episteme), però encara no són objecte de la forma superior d'aquest (la noesis). Per això, solament són objecte de la intel·lecció o pensament discursiu (dianoia). Plató també afirma que la ciència que correspon a CE se sosté en hipòtesi i pressupostos que ella mateixa no estudia, i és tasca del coneixement situat en EC, és a dir, de la filosofia, l'estudi d'aquests primers principis i pressupostos absoluts. Així, el segment que, des del punt de vista ontològic, representa els ens matemàtics, es correspon amb la dianoia. La dianoia té com a objecte d'estudi allò que l'ànima se sent impulsada a estudiar amb ajuda de les imitacions dels primers segments. De la mateixa manera que el subsegmento DC és el model que copia el subsegmento AD, el subsegmento CE és el que serveix de model al mateix DC.

Si es compara aquest text amb la famosa al·legoria de la caverna que es desenvolupa una mica més endavant en el començament del llibre VII de la República (514a-517i) (veure el text del mite de la caverna ), també pot assenyalar-se que cadascun dels segments de la línia es corresponen amb les quatre grans regions en les quals es divideix la realitat descrita per aquest mite. També en la caverna poden distingir-se dues grans regions: la de l'interior de la caverna, i la de l'exterior. La caverna, al seu torn, està poblada per entitats que són manifestament còpies de l'exterior i, en ella, es distingeix la regió en la qual estan encadenats uns presoners obligats a observar solament ombres i la regió que ocupen uns misteriosos personatges que porten escultures il·luminades per un foc. Però si les ombres ho són de les escultures, el foc de l'interior de la caverna és només una molt imperfecta imitació de la llum del sol que està en l'exterior. Així, AC es correspon amb l'interior de la caverna i CB amb l'exterior; AD amb les ombres que veuen els presoners i amb aquests mateixos; DC amb les figures projectades pel foc de la caverna, de les quals les ombres són la seva projecció; CE amb el món exterior del com tot quant està en la caverna és mera còpia i EB amb el sol, sense el qual, com sense les idees, res de quant hi ha en els altres àmbits del real podria ser ja que, com diu Plató, en certa manera, igual que el sol és la causa de les estacions, de la distinció entre el dia i la nit i de l'existència de vida sobre la terra, les idees i, especialment, la idea de Bé és la causa suprema.