Diferència entre revisions de la pàgina «Equivalència (lògica)»
De Wikisofia
| Línia 17: | Línia 17: | ||
</div></div> | </div></div> | ||
| − | En lògica de relacions són equivalents | + | En lògica de relacions són equivalents aquelles relacions que tenen la propietat de ser reflexives, simètriques i transitives (entenent que tota [[relació|relació]] que és simètrica i transitiva és també reflexiva). Les relacions d'equivalència permeten la [[classificació|classificació]]: [[partició|partició]] en grups mútuament excloents. |
{{Etiqueta | {{Etiqueta | ||
Revisió del 22:07, 16 març 2018
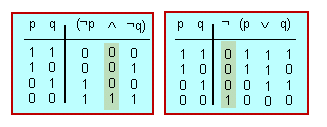
Propietat d'aquelles fórmules que són vertaderes o falses per a idèntiques assignacions de valors de veritat
En lògica de relacions són equivalents aquelles relacions que tenen la propietat de ser reflexives, simètriques i transitives (entenent que tota relació que és simètrica i transitiva és també reflexiva). Les relacions d'equivalència permeten la classificació: partició en grups mútuament excloents.