Diferència entre revisions de la pàgina «Equivalència lògica»
De Wikisofia
| Línia 12: | Línia 12: | ||
«P si i només si Q és veritable quan P i Q són tots dos veritables o tots dos falsos; en els altres casos, és fals». | «P si i només si Q és veritable quan P i Q són tots dos veritables o tots dos falsos; en els altres casos, és fals». | ||
| − | + | ||
| − | + | '''Exemple:''' | |
| − | + | ||
| − | Si p = ets feliç» i q = «estimes», l'enunciat «ets feliç si i només si | + | Si p = ets feliç» i q = «estimes», l'enunciat «ets feliç si i només si estimes», o «ets feliç sempre que estimis» és veritat quan «ets feliç i estimes» i quan «ni ets feliç ni estimes», però és fals si és veritat una d'ambdues coses i no l'altra. |
{{Etiqueta | {{Etiqueta | ||
Revisió del 22:04, 16 març 2018
En lògica d'enunciats, el bicondicional, el signe del qual és: [math]\displaystyle{ \leftrightarrow{} }[/math] i que es llegeix «si, i només si»

Es llegeix, "P si, i només si, Q"
La seva taula de veritat és:
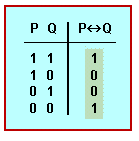
«P si i només si Q és veritable quan P i Q són tots dos veritables o tots dos falsos; en els altres casos, és fals».
Exemple:
Si p = ets feliç» i q = «estimes», l'enunciat «ets feliç si i només si estimes», o «ets feliç sempre que estimis» és veritat quan «ets feliç i estimes» i quan «ni ets feliç ni estimes», però és fals si és veritat una d'ambdues coses i no l'altra.