Diferència entre revisions de la pàgina «Conclusió»
De Wikisofia
m (bot: -tals com +com ara) |
m (bot: - per indicar que + per a indicar que) |
||
| Línia 1: | Línia 1: | ||
{{ConcepteWiki}} | {{ConcepteWiki}} | ||
| − | En els [[raonament|raonaments]] i [[argument]]s, l'[[enunciat|enunciat]] que s'infereix a partir de les [[premisses|premisses]]. La [[inferència|inferència]] que es parla pot ser tant [[deducció|deductiva]] com [[inducció|inductiva]]. En els raonaments informals o semiinformales se sol usar una ratlla horitzontal per indicar que l'enunciat que segueix és la conclusió | + | En els [[raonament|raonaments]] i [[argument]]s, l'[[enunciat|enunciat]] que s'infereix a partir de les [[premisses|premisses]]. La [[inferència|inferència]] que es parla pot ser tant [[deducció|deductiva]] com [[inducció|inductiva]]. En els raonaments informals o semiinformales se sol usar una ratlla horitzontal per a indicar que l'enunciat que segueix és la conclusió |
<div class='mw-collapsible mw-collapsed'> | <div class='mw-collapsible mw-collapsed'> | ||
Revisió de 10:08, 13 oct 2017
En els raonaments i arguments, l'enunciat que s'infereix a partir de les premisses. La inferència que es parla pot ser tant deductiva com inductiva. En els raonaments informals o semiinformales se sol usar una ratlla horitzontal per a indicar que l'enunciat que segueix és la conclusió
- Si dorm, Anna somia
- Anna dorm
- _______________
- Anna somia
- Si Déu no existís tot estaria permès
- Però no és veritat que tot estigui permès
- ___________________________________________
- Per tant, Déu existeix (Dostoyevsky)
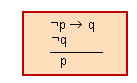
l'esquema lògic del qual és
[math]\displaystyle{ ¬p \rightarrow{q} }[/math]
[math]\displaystyle{ ¬q }[/math]
__________________________________
[math]\displaystyle{ p }[/math]
i en els raonaments del llenguatge ordinari, la presència de la conclusió s'assenyala mitjançant expressions com ara per tant, en conseqüència, per tant, per aquest motiu..., i equivalents.