Diferència entre revisions de la pàgina «Lògiques polivalents»
De Wikisofia
m (bot: -veure text +vegeu el text) |
m (bot: -per vegada primera +per primera vegada) |
||
| Línia 2: | Línia 2: | ||
Lògiques que no es funden en el principi clàssic de [[bivalència, principi de|bivalència]], sinó que atorguen a les [[funció veritativa|funcions veritatives]] valors intermedis entre la veritat i la falsedat. Són lògiques ''finites ''polivalents aquelles que admeten valors intermedis finits, i lògiques ''infinites'' polivalents aquelles que admeten una sèrie infinita de valors intermedis. | Lògiques que no es funden en el principi clàssic de [[bivalència, principi de|bivalència]], sinó que atorguen a les [[funció veritativa|funcions veritatives]] valors intermedis entre la veritat i la falsedat. Són lògiques ''finites ''polivalents aquelles que admeten valors intermedis finits, i lògiques ''infinites'' polivalents aquelles que admeten una sèrie infinita de valors intermedis. | ||
| − | La [[lògica|lògica d'enunciats]] ''trivalente'', desenvolupada per vegada | + | La [[lògica|lògica d'enunciats]] ''trivalente'', desenvolupada per primera vegada per [[Autor:Lukasiewicz, Jan|Lukasiewicz]] ([[Recurs:Lukasiewicz, Jan: els futurs contingents|vegeu el text]]) admet tres [[veritat, valors de|valors de veritat]]: |
Revisió de 09:14, 17 set 2017
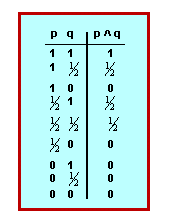
Lògiques que no es funden en el principi clàssic de bivalència, sinó que atorguen a les funcions veritatives valors intermedis entre la veritat i la falsedat. Són lògiques finites polivalents aquelles que admeten valors intermedis finits, i lògiques infinites polivalents aquelles que admeten una sèrie infinita de valors intermedis.
La lògica d'enunciats trivalente, desenvolupada per primera vegada per Lukasiewicz (vegeu el text) admet tres valors de veritat:
Per a aquest tipus de lògica, la taula de veritat corresponent a la definició de la conjunció és la següent: