Diferència entre revisions de la pàgina «Univers del discurs»
De Wikisofia
m (bot: - del com es + del qual es) |
m (bot: - discurs ho forma + discurs el forma) |
||
| Línia 1: | Línia 1: | ||
{{ConcepteWiki}} | {{ConcepteWiki}} | ||
| − | Expressió que es deu a A. de Morgan i que significa la part de l'[[univers|univers]] al fet que ens referim en el discurs, o al conjunt d'objectes que es parla en un determinat context o situació. Així, per exemple, en un llibre de matemàtiques l'univers del discurs són els nombres o les figures geomètriques i en un d'història els successos (les ''res gestae'') de la humanitat, o de part de la humanitat, i de cadascun d'aquests objectes s'afirma i nega alguna cosa. En la [[lògica|lògica de predicats]], l'univers del discurs | + | Expressió que es deu a A. de Morgan i que significa la part de l'[[univers|univers]] al fet que ens referim en el discurs, o al conjunt d'objectes que es parla en un determinat context o situació. Així, per exemple, en un llibre de matemàtiques l'univers del discurs són els nombres o les figures geomètriques i en un d'història els successos (les ''res gestae'') de la humanitat, o de part de la humanitat, i de cadascun d'aquests objectes s'afirma i nega alguna cosa. En la [[lògica|lògica de predicats]], l'univers del discurs el forma qualsevol [[classe (lògica)|classe]] no buida a la qual es refereixen les variables quantificades. Així, en l'expressió |
<math> \forall{x} (Px\rightarrow{}Qx)</math> | <math> \forall{x} (Px\rightarrow{}Qx)</math> | ||
Revisió del 20:26, 29 ago 2017
Expressió que es deu a A. de Morgan i que significa la part de l'univers al fet que ens referim en el discurs, o al conjunt d'objectes que es parla en un determinat context o situació. Així, per exemple, en un llibre de matemàtiques l'univers del discurs són els nombres o les figures geomètriques i en un d'història els successos (les res gestae) de la humanitat, o de part de la humanitat, i de cadascun d'aquests objectes s'afirma i nega alguna cosa. En la lògica de predicats, l'univers del discurs el forma qualsevol classe no buida a la qual es refereixen les variables quantificades. Així, en l'expressió
[math]\displaystyle{ \forall{x} (Px\rightarrow{}Qx) }[/math]
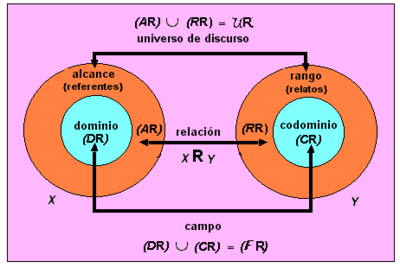
la x es refereix a qualsevol membre o individu de l'univers en general, mentre que a,b,c, etc., indicaria una constant d'individu pertanyent a aquest mateix univers. En lògica de relacions l'univers ho constitueix la summa lògica del conjunt de referents i relats, o d'abast i rang.
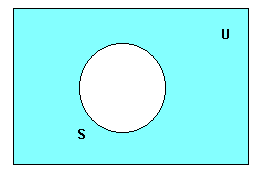
En els diagrames de Venn, l'univers (O) se simbolitza mitjançant el rectangle dins del qual es dibuixen els cercles de les classes