Recurs:Plató: els dos tipus de triangles

Quan déu es va posar a ordenar l'univers, primer va donar forma i nombre al foc, aigua, terra i aire, dels quals, si bé hi havia algunes petjades, es trobaven en l'estat en què probablement es troba tot quan déu està absent. Sigui sempre això el que afirmem en tota ocasió: que déu els va compondre tan bells i excelsos com era possible d'allò que no era així. Ara, en veritat, haig d'intentar demostrar-vos l'ordre i origen de cadascun dels elements amb un discurs poc habitual, però que seguireu perquè per educació podeu recórrer els camins que cal travessar en la demostració.

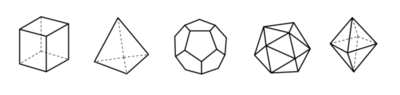
En primer lloc, crec que per a qualsevol està més enllà de tot dubte que foc, terra, aigua i aire són cossos. Ara bé, tota forma corporal té també profunditat. I, a més, és de tota necessitat que la superfície envolti la profunditat. La superfície d'una cara plana està composta de triangles. Tots els triangles es desenvolupen a partir de dos, cadascun amb un angle recte i els altres aguts. Un té a banda i banda una fracció d'angle recte dividit per costats iguals, l'altre parts desiguals d'un angle recte atribuïda a costats desiguals. En la nostra marxa segons el discurs probable acompanyat de necessitat, suposem que aquest és el principi del foc i dels altres cossos. Però els altres principis anteriors a aquests els coneix déu i aquell d'entre els homes que és estimat per ell. Certament, hem d'explicar quins serien els quatre cossos més perfectes, que, encara que dissimiles entre si, podrien néixer els uns dels altres quan es desintegren. En efecte, si ho aconseguim, tindrem la veritat sobre l'origen de la terra i el foc i dels seus mitjans proporcionals. Doncs no coincidirem amb ningú en què hi ha cossos visibles més bells que aquests, dels quals cadascun representa un gènere particular. Hem de, llavors, esforçar-nos per compondre aquests quatre gèneres de cossos d'extraordinària bellesa i dir que hem captat prou la seva naturalesa. Dels dos triangles, a l'isòsceles li va tocar en sort una naturalesa única, però les d'aquell l'angle recte del qual està contingut en costats desiguals van ser infinites. Per a un bon començament cal fer una altra elecció, és necessari triar en la classe dels triangles d'infinites formes aquell que sigui el més perfecte. El que eventualment estigui en condicions d'afirmar que el triangle per ell escollit és el més bell per a la composició dels elements, imposarà la seva opinió, ja que no és un adversari, sinó un amic. Per la nostra banda, nosaltres deixem els altres de costat i suposem que en la multiplicitat dels triangles un és el més bell: aquell del que sorgeix en tercer lloc l'isòsceles. Però especificar el perquè exigeix un raonament major i els premis amistosos jeuen allí pel qual posi a prova aquesta afirmació i descobreixi que és així efectivament. Siguin triats, per tant, dos triangles dels quals estan construïts el cos del foc i el dels altres elements: un d'ells isòsceles, l'altre amb un costat major que el seu quadrat és tres vegades el quadrat del menor. Ara, hem de precisar més el que vam dir abans de manera fosca. Doncs els quatre elements semblaven tenir el seu origen uns d'uns altres, encara que aquesta aparença era falsa, doncs a pesar que els quatre elements neixen dels triangles que hem triat, mentre tres deriven d'un --el que té els costats desiguals--, la cambra és l'únic que es compon del triangle isòsceles. Per tant, no és possible que, mitjançant la dissolució de tots en tots, molts petits donin origen a uns pocs grans i viceversa; però sí que ho és en el cas de tres elements, perquè quan es dissolen els majors d'aquells que per naturalesa estan constituïts per un tipus de triangle, es componen molts petits a partir d'ells, que adopten les figures corresponents i, al seu torn, quan molts petits es dividissin en triangles, en sorgir una quantitat de volum únic, podria donar lloc a una altra forma gran. Aquesta és, doncs, la nostra teoria sobre la gènesi dels uns en els altres. A continuació hauríem de dir de quina manera es va originar la figura de cadascun dels elements i a partir de la unió de quants triangles, En primer lloc, tractaré la figura primera i més petita l'element de la qual és el triangle que té una hipotenusa d'una extensió del doble del costat menor. Quan s'uneixen dos d'aquests per la hipotenusa i això succeeix tres vegades, de manera i que les hipotenuses i els catets menors s'orientin cap a un mateix punt com a centre, es genera un triangle equilàter dels sis. La unió de quatre triangles equilàters segons tres angles plans genera un angle sòlid, el següent del més obtús dels angles plans. Quatre angles d'aquests generen la primera figura sòlida, que divideix tota la superfície de l'esfera en parts iguals i semblants. El segon element es compon dels mateixos triangles quan s'uneixen vuit triangles equilàters i es construeix un angle sòlid a partir de quatre angles plans. Quan s'han generat sis de tals angles, es completa així el segon cos. El tercer cos neix de cent vint elements assemblats i dotze angles sòlids, cadascun envoltat de cinc triangles equilàters plànols i amb vint triangles equilàters per base. La funció d'un dels triangles elementals es va completar quan va generar aquests elements; el triangle isòsceles, d'altra banda, va donar naixement al quart element, per composició de quatre triangles i reunió dels seus angles rectes en el centre per a formar un quadrilàter equilàter. La reunió de sis figures semblants va produir vuit angles sòlids, cadascun d'ells compost segons tres angles plans rectes. La figura del cos creat va ser cúbica amb sis cares de quadrilàters equilàters. ja que encara hi havia una cinquena composició, el déu la va utilitzar per a l'univers quan ho va pintar.

Timeo, 53b-55c. (Traducción de Mª. Ángeles Durán y Francisco Lisi, Diálogos, Vol. VI, Gredos, Madrid 1992, p.206-209).

---

Original en castellà

Cuando dios se puso a ordenar el universo, primero dio forma y número al fuego, agua, tierra y aire, de los que, si bien había algunas huellas, se encontraban en el estado en que probablemente se halle todo cuando dios está ausente. Sea siempre esto lo que afirmamos en toda ocasión: que dios los compuso tan bellos y excelsos como era posible de aquello que no era así. Ahora, en verdad, debo intentar demostraros el orden y origen de cada uno de los elementos con un discurso poco habitual, pero que seguiréis porque por educación podéis recorrer los caminos que hay que atravesar en la demostración.

En primer lugar, creo que para cualquiera está más allá de toda duda que fuego, tierra, agua y aire son cuerpos. Ahora bien, toda forma corporal tiene también profundidad. Y, además, es de toda necesidad que la superficie rodee la profundidad. La superficie de una cara plana está compuesta de triángulos. Todos los triángulos se desarrollan a partir de dos, cada uno con un ángulo recto y los otros agudos. Uno tiene a ambos lados una fracción de ángulo recto dividido por lados iguales, el otro partes desiguales de un ángulo recto atribuida a lados desiguales. En nuestra marcha según el discurso probable acompañado de necesidad, suponemos que éste es el principio del fuego y de los otros cuerpos. Pero los otros principios anteriores a éstos los conoce dios y aquél de entre los hombres que es amado por él. Ciertamente, debemos explicar cuáles serían los cuatro cuerpos más perfectos, que, aunque disímiles entre sí, podrían nacer unos de otros cuando se desintegran. En efecto, si lo logramos, tendremos la verdad acerca del origen de la tierra y el fuego y de sus medios proporcionales. Pues no coincidiremos con nadie en que hay cuerpos visibles más bellos que éstos, de los que cada uno representa un género particular. Debemos, entonces, esforzarnos por componer estos cuatro géneros de cuerpos de extraordinaria belleza y decir que hemos captado su naturaleza suficientemente. De los dos triángulos, al isósceles le tocó en suerte una naturaleza única, pero las de aquel cuyo ángulo recto está contenido en lados desiguales fueron infinitas. Para un buen comienzo hay que hacer otra elección, es necesario elegir en la clase de los triángulos de infinitas formas aquel que sea el más perfecto. El que eventualmente esté en condiciones de afirmar que el triángulo por él escogido es el más bello para la composición de los elementos, impondrá su opinión, puesto que no es un adversario, sino un amigo. Por nuestra parte, nosotros dejamos los demás de lado y suponemos que en la multiplicidad de los triángulos uno es el más bello: aquel del que surge en tercer lugar el isósceles. Pero especificar el porqué exige un razonamiento mayor y los premios amistosos yacen allí para el que ponga a prueba esta afirmación y descubra que es así efectivamente. Sean elegidos, por tanto, dos triángulosde los cuales están construidos el cuerpo del fuego y el de los otros elementos: uno de ellos isósceles, el otro con un lado mayor cuyo cuadrado es tres veces el cuadrado del menor. Ahora, debemos precisar más lo que dijimos antes de manera oscura. Pues los cuatro elementos parecían tener su origen unos de otros, aunque esa apariencia era falsa, pues a pesar de que los cuatro elementos nacen de los triángulos que hemos elegido, mientras tres derivan de uno --el que tiene los lados desiguales--, el cuarto es el único que se compone del triángulo isósceles. Por ende, no es posible que, mediante la disolución de todos en todos, muchos pequeños den origen a unos pocos grandes y viceversa; pero sí lo es en el caso de tres elementos, porque cuando se disuelven los mayores de aquellos que por naturaleza están constituidos por un tipo de triángulo, se componen muchos pequeños a partir de ellos, que adoptan las figuras correspondientes y, a su vez, cuando muchos pequeños se dividieran en triángulos, al surgir una cantidad de volumen único, podría dar lugar a otra forma grande. Ésta es, pues, nuestra teoría acerca de la génesis de unos en otros. A continuación deberíamos decir de qué manera se originó la figura de cada uno de los elementos y a partir de la unión de cuántos triángulos, En primer lugar, trataré la figura primera y más pequeña cuyo elemento es el triángulo que tiene una hipotenusa de una extensión del doble del lado menor. Cuando se unen dos de éstos por la hipotenusa y esto sucede tres veces, de modo e que las hipotenusas y los catetos menores se orienten hacia un mismo punto como centro, se genera un triángulo equilátero de los seis. La unión de cuatro triángulos equiláteros según tres ángulos planos genera un ángulo sólido, el siguiente del más obtuso de los ángulos llanos. Cuatro ángulos de éstos generan la primera figura sólida, que divide toda la superficie de la esfera en partes iguales y semejantes. El segundo elemento se compone de los mismos triángulos cuando se unen ocho triángulos equiláteros y se construye un ángulo sólido a partir de cuatro ángulos planos. Cuando se han generado seis de tales ángulos, se completa así el segundo cuerpo. El tercer cuerpo nace de ciento veinte elementos ensamblados y doce ángulos sólidos, cada uno rodeado de cinco triángulos equiláteros planos y con veinte triángulos equiláteros por base. La función de uno de los triángulos elementales se completó cuando generó estos elementos; el triángulo isósceles, por otra parte, dio nacimiento al cuarto elemento, por composición de cuatro triángulos y reunión de sus ángulos rectos en el centro para formar un cuadrilátero equilátero. La reunión de seis figuras semejantes produjo ocho ángulos sólidos, cada uno de ellos compuesto según tres ángulos planos rectos. La figura del cuerpo creado fue cúbica con seis caras de cuadriláteros equiláteros. Puesto que todavía había una quinta composición, el dios la utilizó para el universo cuando lo pintó.