Diferència entre revisions de la pàgina «Independendencia lògica»
De Wikisofia
(Es crea la pàgina amb «{{ConcepteWiki}} Una fórmula (B) és lògicament independent d'una altra (A) o d'un conjunt de fórmules ()) si i només si no és una conseqüència lògica|conse...».) |
m (Text de reemplaçament - "File:i" a "File:e") |
||
| Línia 10: | Línia 10: | ||
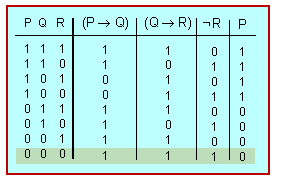
la taula de veritat prova que l'enunciat P és independent de la resta d'enunciats: | la taula de veritat prova que l'enunciat P és independent de la resta d'enunciats: | ||
| − | <center>[[File: | + | <center>[[File:e3491-6.gif]]</center> |
[[Recurs:Exemple d'argument independent]] | [[Recurs:Exemple d'argument independent]] | ||
Revisió de 15:40, 25 abr 2015
Una fórmula (B) és lògicament independent d'una altra (A) o d'un conjunt de fórmules ()) si i només si no és una conseqüència lògica d'elles. B és lògicament independent d'un conjunt ) de fórmules [math]\displaystyle{ (\Delta = A_1, A_2,...A_n = premisses) }[/math] si i només si hi ha alguna interpretació de ) que fa veritable al conjunt ), però no a la conclusió.