Diferència entre revisions de la pàgina «Fórmula vàlida»
De Wikisofia
(Es crea la pàgina amb «{{ConcepteWiki}} O fórmula universalment vàlida. En lògica d'enunciats, aquella que és veritable per qualsevol as...».) |
m (bot: - veritat]] als seus enunciat, + veritat a les seves [[enunciat,) |
||
| (6 revisions intermèdies per 2 usuaris que no es mostren) | |||
| Línia 1: | Línia 1: | ||
{{ConcepteWiki}} | {{ConcepteWiki}} | ||
| − | O [[fórmula universalment vàlida|fórmula universalment vàlida]]. En [[lògica|lògica d'enunciats]], aquella que és veritable per qualsevol [[assignació|assignació]] de [[veritat, valors de|valor de veritat]] | + | O [[fórmula universalment vàlida|fórmula universalment vàlida]]. En [[lògica|lògica d'enunciats]], aquella que és veritable per qualsevol [[assignació|assignació]] de [[veritat, valors de|valor de veritat]] a les seves [[enunciat, lletres d'|lletres d'enunciat]]; una fórmula universalment vàlida és també una [[tautologia|tautologia]], doncs el seu valor en una [[lògica|taula de veritat]] és sempre veritable, però, a vegades, es diu preferentment «vàlida» a una fórmula i «[[tautologia|tautologia]]» a un enunciat. |
<div class='mw-collapsible mw-collapsed'> | <div class='mw-collapsible mw-collapsed'> | ||
| − | <center>''' | + | <center>'''Veg. exemple ↓'''</center> |
<div class="mw-collapsible-content"> | <div class="mw-collapsible-content"> | ||
| Línia 10: | Línia 10: | ||
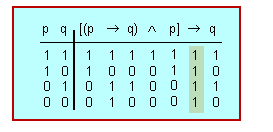
és una ''fórmula'' universalment vàlida: | és una ''fórmula'' universalment vàlida: | ||
| − | [[File: | + | [[File:e1630-1.gif]] |
mentre que «ser o no ser» és un ''enunciat ''tautològic, o una tautologia.</center> | mentre que «ser o no ser» és un ''enunciat ''tautològic, o una tautologia.</center> | ||
| Línia 20: | Línia 20: | ||
<div class='mw-collapsible mw-collapsed'> | <div class='mw-collapsible mw-collapsed'> | ||
| − | <center>''' | + | <center>'''Veg. exemple ↓'''</center> |
<div class="mw-collapsible-content"> | <div class="mw-collapsible-content"> | ||
| − | D'un enunciat com <math>\forall{x} Px</math> pot deduir-se <math>\exists{x} Px</math>, i aquesta deducció pot fer-se sense premisses. Per tant, és possible escriure <math>\vdash \forall{x} Px \rightarrow{\exists{x} Px}</math> i, | + | D'un enunciat com <math>\forall{x} Px</math> pot deduir-se <math>\exists{x} Px</math>, i aquesta deducció pot fer-se sense premisses. Per tant, és possible escriure <math>\vdash \forall{x} Px \rightarrow{\exists{x} Px}</math> i, per aquesta raó, suposar que <math>\models \forall{x} Px \rightarrow{\exists{x} Px}</math>. |
Però aquesta última fórmula, encara que necessàriament veritable, no és una tautologia. La seva veritat es demostra només com a conclusió d'una demostració o derivació. | Però aquesta última fórmula, encara que necessàriament veritable, no és una tautologia. La seva veritat es demostra només com a conclusió d'una demostració o derivació. | ||
| − | [[Recurs:Exemple de fórmula vàlida no | + | [[Recurs:Exemple de fórmula vàlida no tautològica]] |
</div></div> | </div></div> | ||
Revisió de 14:36, 29 ago 2017
O fórmula universalment vàlida. En lògica d'enunciats, aquella que és veritable per qualsevol assignació de valor de veritat a les seves lletres d'enunciat; una fórmula universalment vàlida és també una tautologia, doncs el seu valor en una taula de veritat és sempre veritable, però, a vegades, es diu preferentment «vàlida» a una fórmula i «tautologia» a un enunciat.
és una fórmula universalment vàlida:
mentre que «ser o no ser» és un enunciat tautològic, o una tautologia.Recurs:Exemple de fórmula universalment vàlida per a tota assignació
En lògica de predicats, és universalment vàlida aquella fórmula que no pot ser falsa; però no tota fórmula vàlida és una tautologia.
D'un enunciat com [math]\displaystyle{ \forall{x} Px }[/math] pot deduir-se [math]\displaystyle{ \exists{x} Px }[/math], i aquesta deducció pot fer-se sense premisses. Per tant, és possible escriure [math]\displaystyle{ \vdash \forall{x} Px \rightarrow{\exists{x} Px} }[/math] i, per aquesta raó, suposar que [math]\displaystyle{ \models \forall{x} Px \rightarrow{\exists{x} Px} }[/math].
Però aquesta última fórmula, encara que necessàriament veritable, no és una tautologia. La seva veritat es demostra només com a conclusió d'una demostració o derivació.