Diferència entre revisions de la pàgina «Taula de veritat d'un raonament»
De Wikisofia
| (Una revisió intermèdia per un altre usuari que no es mostra) | |||
| Línia 10: | Línia 10: | ||
Sigui el següent raonament: | Sigui el següent raonament: | ||
| − | «Si | + | «Si somio, desitjo, i si estic despert, em deleixo, i o somio o estic despert; per tant o desitjo o em deleixo», la formalització del qual pot ser: |
| + | <center> <math>[[(p\rightarrow q)]\wedge (r\rightarrow s)]\wedge (p\vee r)]\rightarrow q\vee s</math></center> | ||
la taula de veritat d'aquest «dilema constructiu» és la següent: | la taula de veritat d'aquest «dilema constructiu» és la següent: | ||
| Línia 16: | Línia 17: | ||
<center>[[File:e3671-4.gif]]</center> | <center>[[File:e3671-4.gif]]</center> | ||
| − | La taula mostra que, sempre que les premisses són | + | La taula mostra que, sempre que les premisses són vertaderes, la conclusió també és vertadera, i no succeeix que les premisses siguin vertaderesi la conclusió falsa. La taula mostra que el «dilema constructiu» és un raonament vàlid. |
{{InfoWiki}} | {{InfoWiki}} | ||
Revisió de 21:14, 21 feb 2018
Sigui el següent raonament:
«Si somio, desitjo, i si estic despert, em deleixo, i o somio o estic despert; per tant o desitjo o em deleixo», la formalització del qual pot ser:
la taula de veritat d'aquest «dilema constructiu» és la següent:
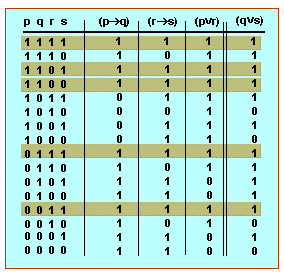
La taula mostra que, sempre que les premisses són vertaderes, la conclusió també és vertadera, i no succeeix que les premisses siguin vertaderesi la conclusió falsa. La taula mostra que el «dilema constructiu» és un raonament vàlid.