Diferència entre revisions de la pàgina «Assignació»
De Wikisofia
m (Text de reemplaçament - "File:i" a "File:e") |
m (bot: -veure exemple +veg. exemple) |
||
| (Una revisió intermèdia per un altre usuari que no es mostra) | |||
| Línia 5: | Línia 5: | ||
<div class='mw-collapsible mw-collapsed'> | <div class='mw-collapsible mw-collapsed'> | ||
| − | <center>''' | + | <center>'''veg. exemple ↓'''</center> |
<div class="mw-collapsible-content"> | <div class="mw-collapsible-content"> | ||
<math>[(p \rightarrow{q})\wedge p]\rightarrow{q}</math> | <math>[(p \rightarrow{q})\wedge p]\rightarrow{q}</math> | ||
| Línia 22: | Línia 22: | ||
<div class='mw-collapsible mw-collapsed'> | <div class='mw-collapsible mw-collapsed'> | ||
| − | <center>''' | + | <center>'''veg. exemple ↓'''</center> |
<div class="mw-collapsible-content"> | <div class="mw-collapsible-content"> | ||
<math>[(p \wedge q) \wedge (¬p \wedge ¬q)]</math> | <math>[(p \wedge q) \wedge (¬p \wedge ¬q)]</math> | ||
| Línia 30: | Línia 30: | ||
[[File:e5010-1.gif]] | [[File:e5010-1.gif]] | ||
| − | ([[Recurs:Exemple lògic de fórmula contradictòria| | + | ([[Recurs:Exemple lògic de fórmula contradictòria|veg. exemple]]) |
</div></div> | </div></div> | ||
| Línia 37: | Línia 37: | ||
<div class='mw-collapsible mw-collapsed'> | <div class='mw-collapsible mw-collapsed'> | ||
| − | <center>''' | + | <center>'''veg. exemple ↓'''</center> |
<div class="mw-collapsible-content"> | <div class="mw-collapsible-content"> | ||
<center><math>[(p \wedge q) \vee (¬p\wedge q)]</math></center> | <center><math>[(p \wedge q) \vee (¬p\wedge q)]</math></center> | ||
| Línia 43: | Línia 43: | ||
<center>és una fórmula consistent</center> | <center>és una fórmula consistent</center> | ||
| − | <center>[[Image: | + | <center>[[Image:e5010-2.png|400px]]</center> |
| − | ([[Recurs:Exemple lògic de fórmula consistent| | + | ([[Recurs:Exemple lògic de fórmula consistent|veg. exemple]]). |
</div></div> | </div></div> | ||
| Línia 54: | Línia 54: | ||
<div class='mw-collapsible mw-collapsed'> | <div class='mw-collapsible mw-collapsed'> | ||
| − | <center>''' | + | <center>'''veg. exemple ↓'''</center> |
<div class="mw-collapsible-content"> | <div class="mw-collapsible-content"> | ||
<center><math>(¬p \wedge ¬q)</math> i <math>¬(p \vee q)</math></center> | <center><math>(¬p \wedge ¬q)</math> i <math>¬(p \vee q)</math></center> | ||
| Línia 64: | Línia 64: | ||
<center>[[File:e5010-3.gif]]</center> | <center>[[File:e5010-3.gif]]</center> | ||
| − | ([[Recurs:Exemple lògic de fórmules equivalents| | + | ([[Recurs:Exemple lògic de fórmules equivalents|veg. exemple]]). |
</div></div> | </div></div> | ||
Revisió de 11:55, 22 ago 2017
Valors que es donen a les lletres d'enunciat d'una fórmula de manera que aquesta és:
universalment vàlida si és veritable per a tota assignació.
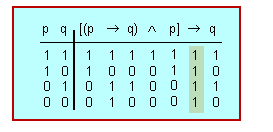
[math]\displaystyle{ [(p \rightarrow{q})\wedge p]\rightarrow{q} }[/math]
és una fórmula universalment vàlida:
mentre que «ser o no ser» és un enunciat tautològic, o una tautologia.
Recurs:Exemple de fórmula universalment vàlida per a tota assignació
contradictòria, si és falsa per a tota assignació
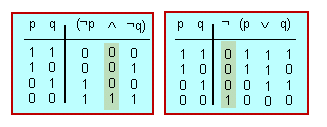
[math]\displaystyle{ [(p \wedge q) \wedge (¬p \wedge ¬q)] }[/math]
és una fórmula contradictòria
i consistent, si és veritable almenys per a una assignació.

(veg. exemple).
Es dedueix que tota fórmula vàlida és, a més, consistent, però no al revés.
Dues fórmules són equivalents, si cobren igual valor per a idèntiques assignacions o reben els mateixos valors en una taula de veritat.
(veg. exemple).