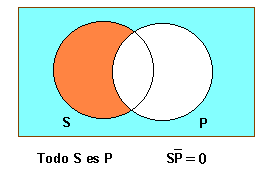Diferència entre revisions de la pàgina «Sil·logística»
De Wikisofia
m (bot: - ualitat|qualitat]], això és, + ualitat|qualitat]], és a dir,) |
|||
| (15 revisions intermèdies per 2 usuaris que no es mostren) | |||
| Línia 1: | Línia 1: | ||
{{ConcepteWiki}} | {{ConcepteWiki}} | ||
| − | Teoria de la [[lògica|lògica]] tradicional sobre el [[sil·logisme|sil·logisme]]. La teoria és exposada per vegada | + | Teoria de la [[lògica|lògica]] tradicional sobre el [[sil·logisme|sil·logisme]]. La teoria és exposada per primera vegada en l'obra d'[[Autor:Aristòtil|Aristòtil]], ''Analítics primers'', es desenvolupa al llarg de l'edat mitjana, en la [[filosofia escolàstica|filosofia escolàstica]], i el seu estudi i desenvolupament constitueix la part més important de la lògica antiga. Alguns filòsofs, com Bacon, Descartes, J.S. Mill i uns altres, l'han constituït en objecte preferent de les seves crítiques, per a considerar que les seves demostracions són una mera [[petició de principi|petició de principi]], però no deixa de ser la part de la lògica més venerable i tradicional, en la qual s'han exercitat la major part de ments il·lustres i, posada en relació amb altres parts de la lògica, no deixa de ser una de les seves qüestions més centrals. La lògica moderna, d'altra banda, li ha dedicat [[sistema axiomàtic|sistemes axiomàtics]] formalitzats. |
Si se la contempla des de la perspectiva de la [[lògica|lògica de classes]], un sil·logisme suposa relacions d'inclusió i intersecció entre tres classes: les representades pel [[terme|terme]] subjecte, el terme predicat i el terme mitjà. | Si se la contempla des de la perspectiva de la [[lògica|lògica de classes]], un sil·logisme suposa relacions d'inclusió i intersecció entre tres classes: les representades pel [[terme|terme]] subjecte, el terme predicat i el terme mitjà. | ||
| Línia 8: | Línia 8: | ||
Si se la contempla des de la perspectiva de la [[lògica cuantificacional|lògica cuantificacional]], un sil·logisme categòric és un raonament compost per enunciats quantificats (pels quantificadors «tots» i «alguns», o generalitzador i particularitzador) que impliquen la conclusió. | Si se la contempla des de la perspectiva de la [[lògica cuantificacional|lògica cuantificacional]], un sil·logisme categòric és un raonament compost per enunciats quantificats (pels quantificadors «tots» i «alguns», o generalitzador i particularitzador) que impliquen la conclusió. | ||
| − | Com [[lògica|lògica de predicats]], o de termes, analitza l'estructura de conjunts d'enunciats composts de subjecte, còpula verbal i predicat, que constitueixen raonaments. El raonament basat en [[enunciat categòric|enunciats categòrics]] es diu [[sil·logisme|sil·logisme]] categòric, compost per | + | Com [[lògica|lògica de predicats]], o de termes, analitza l'estructura de conjunts d'enunciats composts de subjecte, còpula verbal i predicat, que constitueixen raonaments. El raonament basat en [[enunciat categòric|enunciats categòrics]] es diu [[sil·logisme|sil·logisme]] categòric, compost per dues [[premisses|premisses]] i una [[conclusió|conclusió]]. Les premisses contenen, a més del [[subjecte |subjecte]] i el [[predicat|predicat]], un terme comú a ambdues, o mitjà, mentre que la conclusió es compon del subjecte d'una de les premisses i del predicat de l'altra, desapareixent el terme mitjà |
<div class='mw-collapsible mw-collapsed'> | <div class='mw-collapsible mw-collapsed'> | ||
| − | <center>''' | + | <center>'''veg. exemple ↓'''</center> |
<div class="mw-collapsible-content"> | <div class="mw-collapsible-content"> | ||
:Cap quadrúpede sap xiular | :Cap quadrúpede sap xiular | ||
| Línia 27: | Línia 27: | ||
</div></div> | </div></div> | ||
| − | En un sil·logisme, com el | + | En un sil·logisme, com el següent: |
:Tots els homes són mortals | :Tots els homes són mortals | ||
| Línia 44: | Línia 44: | ||
[[File:3350-3.png|400px]] | [[File:3350-3.png|400px]] | ||
| − | I atès que cadascun dels enunciats categòrics, que componen les premisses i la conclusió, pot variar segons la [[quantitat|quantitat]] i la [[qualitat|qualitat]], | + | I atès que cadascun dels enunciats categòrics, que componen les premisses i la conclusió, pot variar segons la [[quantitat|quantitat]] i la [[qualitat|qualitat]], és a dir, poden ser universals o particulars i afirmatius o negatius, les quatre figures donen un total de 256 combinacions possibles, o ''maneres'', dels quals només 19 es consideren sil·logismes [[validesa|vàlids]] o correctes |
<div class='mw-collapsible mw-collapsed'> | <div class='mw-collapsible mw-collapsed'> | ||
| − | <center>''' | + | <center>'''veg. exemple ↓'''</center> |
<div class="mw-collapsible-content"> | <div class="mw-collapsible-content"> | ||
| Línia 53: | Línia 53: | ||
:Totes les criatures brunzents són molestes | :Totes les criatures brunzents són molestes | ||
| − | : | + | :Tots els mosquits són brunzents |
:__________________________________ | :__________________________________ | ||
| − | : | + | :Tots els mosquits són molests |
| Línia 61: | Línia 61: | ||
:Tots els que canten com a canaris són melodiosos | :Tots els que canten com a canaris són melodiosos | ||
| − | :Cap cigne és | + | :Cap cigne és melodiós |
:___________________________________________ | :___________________________________________ | ||
:Cap cigne canta com un canari | :Cap cigne canta com un canari | ||
| Línia 101: | Línia 101: | ||
<div class='mw-collapsible mw-collapsed'> | <div class='mw-collapsible mw-collapsed'> | ||
| − | <center>''' | + | <center>'''veg. exemple ↓'''</center> |
<div class="mw-collapsible-content"> | <div class="mw-collapsible-content"> | ||
En l'exemple de Lewis Carroll: | En l'exemple de Lewis Carroll: | ||
| Línia 125: | Línia 125: | ||
<div class='mw-collapsible mw-collapsed'> | <div class='mw-collapsible mw-collapsed'> | ||
| − | <center>''' | + | <center>'''veg. exemple ↓'''</center> |
<div class="mw-collapsible-content"> | <div class="mw-collapsible-content"> | ||
| Línia 146: | Línia 146: | ||
[[Recurs:Diagrames de Venn i classes d'enunciats|exemple]] | [[Recurs:Diagrames de Venn i classes d'enunciats|exemple]] | ||
</div></div> | </div></div> | ||
| − | , i la qüestió de la [[validesa|validesa]] dels | + | , i la qüestió de la [[validesa|validesa]] dels raonaments sil·logístics pot resoldre's mitjançant aquests mateixos diagrames |
<div class='mw-collapsible mw-collapsed'> | <div class='mw-collapsible mw-collapsed'> | ||
| − | <center>''' | + | <center>'''veg. exemple ↓'''</center> |
<div class="mw-collapsible-content"> | <div class="mw-collapsible-content"> | ||
| − | [[File: | + | [[File:e3682-2.png|500]] |
La conclusió correcta hauria de ser: | La conclusió correcta hauria de ser: | ||
| Línia 158: | Línia 158: | ||
«Algunes criatures feres no beuen cafè». | «Algunes criatures feres no beuen cafè». | ||
| − | ([[Recurs:Exemple de sil·logisme: diagrames de Venn| | + | ([[Recurs:Exemple de sil·logisme: diagrames de Venn|veg. exemple]]). |
</div></div> | </div></div> | ||
Si contemplem els sil·logismes des de la perspectiva de la lògica d'enunciats, poden considerar-se com una implicació, que el seu antecedent és una conjunció. La seva validesa, en aquest cas, pot demostrar-se amb les [[lògica|taules de veritat]]: | Si contemplem els sil·logismes des de la perspectiva de la lògica d'enunciats, poden considerar-se com una implicació, que el seu antecedent és una conjunció. La seva validesa, en aquest cas, pot demostrar-se amb les [[lògica|taules de veritat]]: | ||
| − | Així, l'exemple abans proposat és una | + | Així, l'exemple abans proposat és una tautologia: |
[[File:3350-9.png|400px]] | [[File:3350-9.png|400px]] | ||
| Línia 174: | Línia 174: | ||
<div class='mw-collapsible mw-collapsed'> | <div class='mw-collapsible mw-collapsed'> | ||
| − | <center>''' | + | <center>'''veg. exemple ↓'''</center> |
<div class="mw-collapsible-content"> | <div class="mw-collapsible-content"> | ||
El sil·logisme de la primera figura: | El sil·logisme de la primera figura: | ||
| Línia 213: | Línia 213: | ||
| − | En eliminar el particularitzador en la línia 4, ha d'iniciar-se una subderivació que permeti introduir, com succeeix en la línia 9, el quantificador existencial. Així es compleix la condició '''*2''', de les regles del càlcul de la lògica de predicats ( | + | En eliminar el particularitzador en la línia 4, ha d'iniciar-se una subderivació que permeti introduir, com succeeix en la línia 9, el quantificador existencial. Així es compleix la condició '''*2''', de les regles del càlcul de la lògica de predicats (veg. les regles al final). |
El sil·logisme de la quarta figura: | El sil·logisme de la quarta figura: | ||
| Línia 232: | Línia 232: | ||
<center>[[File:2315F.png|400px]]</center> | <center>[[File:2315F.png|400px]]</center> | ||
| − | [[Recurs:Exemple de sil·logisme i lògica de | + | [[Recurs:Exemple de sil·logisme i lògica de quantors|exemple]] |
</div></div> | </div></div> | ||
Revisió de 13:24, 4 juny 2018
Teoria de la lògica tradicional sobre el sil·logisme. La teoria és exposada per primera vegada en l'obra d'Aristòtil, Analítics primers, es desenvolupa al llarg de l'edat mitjana, en la filosofia escolàstica, i el seu estudi i desenvolupament constitueix la part més important de la lògica antiga. Alguns filòsofs, com Bacon, Descartes, J.S. Mill i uns altres, l'han constituït en objecte preferent de les seves crítiques, per a considerar que les seves demostracions són una mera petició de principi, però no deixa de ser la part de la lògica més venerable i tradicional, en la qual s'han exercitat la major part de ments il·lustres i, posada en relació amb altres parts de la lògica, no deixa de ser una de les seves qüestions més centrals. La lògica moderna, d'altra banda, li ha dedicat sistemes axiomàtics formalitzats.
Si se la contempla des de la perspectiva de la lògica de classes, un sil·logisme suposa relacions d'inclusió i intersecció entre tres classes: les representades pel terme subjecte, el terme predicat i el terme mitjà.
Si se la contempla des de la perspectiva de la lògica d'enunciats, un sil·logisme és un condicional format per la conjunció de les premisses que impliquen a la conclusió.
Si se la contempla des de la perspectiva de la lògica cuantificacional, un sil·logisme categòric és un raonament compost per enunciats quantificats (pels quantificadors «tots» i «alguns», o generalitzador i particularitzador) que impliquen la conclusió.
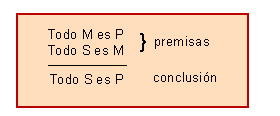
Com lògica de predicats, o de termes, analitza l'estructura de conjunts d'enunciats composts de subjecte, còpula verbal i predicat, que constitueixen raonaments. El raonament basat en enunciats categòrics es diu sil·logisme categòric, compost per dues premisses i una conclusió. Les premisses contenen, a més del subjecte i el predicat, un terme comú a ambdues, o mitjà, mentre que la conclusió es compon del subjecte d'una de les premisses i del predicat de l'altra, desapareixent el terme mitjà
- Cap quadrúpede sap xiular
- Alguns gats són quadrúpedes
- ________________________________________
- Alguns gats no saben xiular (L. Carroll)
- Cap fòssil pot estar traspassat d'amor
- Una ostra pot estar traspassada d'amor
- ____________________________________
- Les ostres no són fòssils (L. Carroll)
En un sil·logisme, com el següent:
- Tots els homes són mortals
- Els filòsofs són homes
- _______________________________________
- Per tant, els filòsofs són mortals
s'observa el següent esquema lògic:
on S, «filòsofs», és el terme subjecte, P, «mortals», el terme predicat i M, «homes», el terme mitjà.
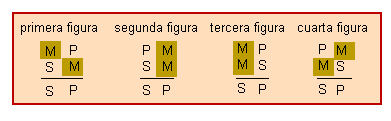
Segons el ja que ocupa el terme mitjà, es distingeix quatre figures del sil·logisme
I atès que cadascun dels enunciats categòrics, que componen les premisses i la conclusió, pot variar segons la quantitat i la qualitat, és a dir, poden ser universals o particulars i afirmatius o negatius, les quatre figures donen un total de 256 combinacions possibles, o maneres, dels quals només 19 es consideren sil·logismes vàlids o correctes
De la primera figura:
- Totes les criatures brunzents són molestes
- Tots els mosquits són brunzents
- __________________________________
- Tots els mosquits són molests
De la segona figura:
- Tots els que canten com a canaris són melodiosos
- Cap cigne és melodiós
- ___________________________________________
- Cap cigne canta com un canari
De la tercera figura:
- Tots els lleons són reis de la selva
- Alguns lleons són exhibits en el circ
- ________________________________________________
- Alguns animals exhibits en el circ són reis de la selva
De la quarta figura:
- Cap fòssil canta cançons romàntiques
- Algú que canta cançons romàntiques és sensible
- ___________________________________________
- Algú sensible no és un fòssil
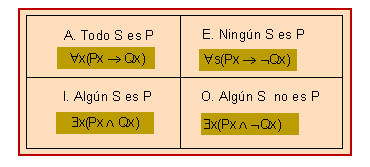
Recordant que els tipus d'enunciats categòrics s'exemplifiquen mitjançant les lletres A, I, I i O, les maneres vàlides són els següents:
La validesa dels sil·logismes exigeix l'observança de diverses regles:
1. Almenys una premissa ha de ser afirmativa
2. Si una premissa és negativa, la conclusió ha de ser negativa.
3. Si una premissa és particular, la conclusió ha de ser particular.
4. El terme mitjà ha de ser universal almenys una vegada.
5. Si un terme és universal en la conclusió, ho ha de ser també en la premissa corresponent
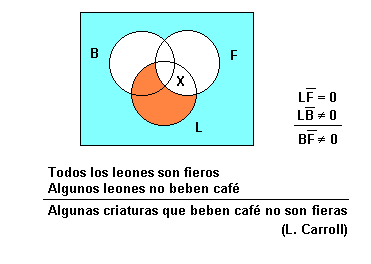
En l'exemple de Lewis Carroll:
- Tots els lleons són fers
- Alguns lleons no beuen cafè
- _____________________________________________
- Algunes criatures que beuen cafè no són feres
La conclusió és incorrecta (hauria de ser «algunes criatures feres no beuen cafè») perquè no compleix amb la regla 4: un terme que es pren en la seva accepció universal en la conclusió («no són feres»), s'ha pres com a particular en la premissa major.
La conclusió correcta hauria de ser:
«Algunes criatures feres no beuen cafè».
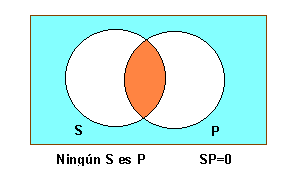
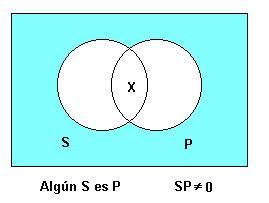
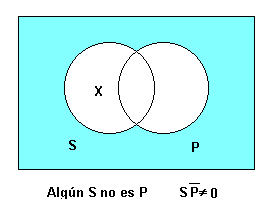
ja que els termes, subjecte i predicat, d'un enunciat designen classes, un sil·logisme pot interpretar-se com una relació entre classes; els seus enunciats poden representar-se mitjançant els diagrames de Venn
, i la qüestió de la validesa dels raonaments sil·logístics pot resoldre's mitjançant aquests mateixos diagrames
Si contemplem els sil·logismes des de la perspectiva de la lògica d'enunciats, poden considerar-se com una implicació, que el seu antecedent és una conjunció. La seva validesa, en aquest cas, pot demostrar-se amb les taules de veritat:
Així, l'exemple abans proposat és una tautologia:
Els enunciats categòrics poden ser també vists des de la lògica de quantificadors, passant a adquirir la següent forma lògica:
En aquest cas, la validesa dels sil·logismes es resol recorrent a la lògica cuantificacional o lògica de cuantores
El sil·logisme de la primera figura:
- Totes les criatures brunzents són mal acollides
- Tots els mosquits són brunzents
- _____________________________________
- Tots els mosquits són mal acollits
pot resoldre's de la següent manera:
El sil·logisme de la segona figura:
- Tots els que canten com a canaris són melodiosos
- Cap cigne és melodioso
- ___________________________________________
- Cap cigne canta com un canari
pot escriure's com:
El sil·logisme de la tercera figura:
- Tots els lleons són fers
- Alguns lleons són exhibits en el circ
- _________________________________
- Alguns animals exhibits en el circ són fers
pot escriure's de la següent manera:
En eliminar el particularitzador en la línia 4, ha d'iniciar-se una subderivació que permeti introduir, com succeeix en la línia 9, el quantificador existencial. Així es compleix la condició *2, de les regles del càlcul de la lògica de predicats (veg. les regles al final).
El sil·logisme de la quarta figura:
- Cap rondalla és terrible
- Hi ha coses terribles que són seductores
- __________________________________
- Hi ha coses seductores que no són rondalles
pot escriure's de la següent manera:
En eliminar el particularitzador en la línia 4, ha d'iniciar-se una subderivació que permeti introduir, com succeeix en la línia 9, el quantificador existencial. Així es compleix la condició *2, de les regles del càlcul de la lògica de predicats (segons les regles que es mostren a continuació).