Diferència entre revisions de la pàgina «Reducció a l'absurd»
De Wikisofia
m (bot: -veure exemple +veg. exemple) |
|||
| (8 revisions intermèdies per 2 usuaris que no es mostren) | |||
| Línia 2: | Línia 2: | ||
<small>(del llatí ''reductio ad absurdum'')</small> | <small>(del llatí ''reductio ad absurdum'')</small> | ||
| − | [[raonament|Raonament]] que es basa a demostrar que un conjunt d'afirmacions format per les [[premisses|premisses]] i la negació de la seva [[conclusió|conclusió]] porta a una [[contradicció|contradicció]] ([[esquema lògic d'una reducció a l'absurd|veg. exemple]]). Equival a raonar de la següent manera: si el fet de suposar veritable ¬A (no-A) ens porta a una contradicció, llavors A és necessàriament veritable i ¬A necessàriament falsa. Rep també el nom de [[prova indirecta|prova indirecta]]. De vegades, la reducció a l'absurd només prova que un conjunt de premisses és inconsistent. | + | [[raonament|Raonament]] que es basa a demostrar que un conjunt d'afirmacions format per les [[premisses|premisses]] i la negació de la seva [[conclusió|conclusió]] porta a una [[contradicció|contradicció]] ([[esquema lògic d'una reducció a l'absurd|veg. exemple]]). Equival a raonar de la següent manera: si el fet de suposar veritable ¬A (no-A) ens porta a una contradicció, llavors A és necessàriament veritable i ¬A necessàriament falsa. Rep també el nom de [[prova indirecta|prova indirecta]]. De vegades, la reducció a l'[[absurd]] només prova que un conjunt de premisses és inconsistent. |
<div class='mw-collapsible mw-collapsed'> | <div class='mw-collapsible mw-collapsed'> | ||
| − | <center>''' | + | <center>'''Veg. exemple →'''</center> |
<div class="mw-collapsible-content"> | <div class="mw-collapsible-content"> | ||
1. Déu és omnipotent. | 1. Déu és omnipotent. | ||
| Línia 15: | Línia 15: | ||
4. Si Déu és omnipotent, Déu pot crear tot el que pot ser pensat. | 4. Si Déu és omnipotent, Déu pot crear tot el que pot ser pensat. | ||
| − | 5. Si Déu és omnipotent, tot | + | 5. Si Déu és omnipotent, tot el que pot crear el pot també destruir. |
6. És possible pensar en una entitat indestructible (aquella precisament que posseeix la propietat de no poder ser destruïda). | 6. És possible pensar en una entitat indestructible (aquella precisament que posseeix la propietat de no poder ser destruïda). | ||
| Línia 30: | Línia 30: | ||
9. Déu pot pensar en una entitat indestructible | 9. Déu pot pensar en una entitat indestructible | ||
| − | 10. Tot | + | 10. Tot el que Déu pot pensar pot també crear-ho. |
11. Si Déu pot pensar en una entitat indestructible, també pot crear una entitat indestructible. | 11. Si Déu pot pensar en una entitat indestructible, també pot crear una entitat indestructible. | ||
| Línia 36: | Línia 36: | ||
12. Déu pot crear una entitat indestructible. | 12. Déu pot crear una entitat indestructible. | ||
| − | 13. Però tot | + | 13. Però tot el que Déu pot crear també pot destruir-ho. |
14. En concret, si Déu pot crear una entitat indestructible, llavors Déu pot destruir una entitat indestructible. | 14. En concret, si Déu pot crear una entitat indestructible, llavors Déu pot destruir una entitat indestructible. | ||
| Línia 45: | Línia 45: | ||
_____________________________________________________________ | _____________________________________________________________ | ||
| − | {{Ref|Ref=Pres de W. Neblet, ''Sherlock's Logic'', University Press of America, Lanham-Nova York-Londres 1985, p. 127-128 trad. catal.: ''La lògica de Sherlock Holmes'', La Magrana, Barcelona 1989, p. 125-126). | + | |
| + | {{Ref|Ref=Pres de W. Neblet, ''Sherlock's Logic'', University Press of America, Lanham-Nova York-Londres 1985, p. 127-128 trad. catal.: ''La lògica de Sherlock Holmes'', La Magrana, Barcelona 1989, p. 125-126).|Cita=true}} | ||
| + | |||
</div></div> | </div></div> | ||
Històricament, l'ús de raonaments indirectes és normal en geometria; les [[paradoxes de Zenó|paradoxes de Zenó]] han estat contemplades també com a raonaments per reducció a l'absurd. | Històricament, l'ús de raonaments indirectes és normal en geometria; les [[paradoxes de Zenó|paradoxes de Zenó]] han estat contemplades també com a raonaments per reducció a l'absurd. | ||
| + | |||
| + | ---- | ||
| + | '''L'esquema lògic d'una reducció a l'absurd és el següent:''' | ||
| + | {|class="wikitable" style="width: 30%;" | ||
| + | | style="width: 10%"|<math> | ||
| + | p\\ | ||
| + | .\\ | ||
| + | .\\ | ||
| + | .\\ | ||
| + | q\wedge \neg q\\ </math> | ||
| + | ____________ | ||
| + | |||
| + | <math> | ||
| + | \neg p | ||
| + | </math> | ||
| + | | style="width: 50%"|Això vol dir que si suposem ''p'' i finalment arribem a una contradicció com <math>q\wedge \neg q</math>, llavors hem de concloure la negació de la suposició ''p'', per tant <math>\neg p</math> | ||
| + | |} | ||
| + | |||
| + | ---- | ||
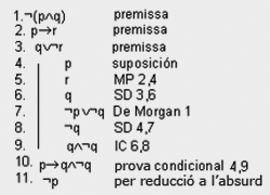
| + | Suposem que es vol demostrar que «Raül no és magnànim» a partir de les premisses: | ||
| + | |||
| + | 1. No és possible que Raül sigui magnànim i sever al mateix temps. | ||
| + | |||
| + | 2. Si Raül és magnànim, perdona. | ||
| + | |||
| + | 3. O Raül és sever o no perdona. | ||
| + | |||
| + | [[Image:E3149-1Bcat.png|300px]] | ||
| + | |||
| + | Veg. [[Apagoge]]. | ||
| + | |||
| + | [[Recurs:Exemple prova indirecta: existència de Déu|Veg. exemple]]. | ||
| − | |||
Revisió de 19:06, 9 feb 2020
(del llatí reductio ad absurdum)
Raonament que es basa a demostrar que un conjunt d'afirmacions format per les premisses i la negació de la seva conclusió porta a una contradicció (veg. exemple). Equival a raonar de la següent manera: si el fet de suposar veritable ¬A (no-A) ens porta a una contradicció, llavors A és necessàriament veritable i ¬A necessàriament falsa. Rep també el nom de prova indirecta. De vegades, la reducció a l'absurd només prova que un conjunt de premisses és inconsistent.
1. Déu és omnipotent.
2. Déu és omniscient.
3. Si Déu és omniscient, Déu pot pensar en tot el que pot ser pensat.
4. Si Déu és omnipotent, Déu pot crear tot el que pot ser pensat.
5. Si Déu és omnipotent, tot el que pot crear el pot també destruir.
6. És possible pensar en una entitat indestructible (aquella precisament que posseeix la propietat de no poder ser destruïda).
_________________________________________________________________
Per tant,
7. Déu pot pensar en tot el que pot ser pensat.
8. En concret, si una entitat indestructible pot ser pensada, Déu pot pensar-la.
9. Déu pot pensar en una entitat indestructible
10. Tot el que Déu pot pensar pot també crear-ho.
11. Si Déu pot pensar en una entitat indestructible, també pot crear una entitat indestructible.
12. Déu pot crear una entitat indestructible.
13. Però tot el que Déu pot crear també pot destruir-ho.
14. En concret, si Déu pot crear una entitat indestructible, llavors Déu pot destruir una entitat indestructible.
15. Déu pot destruir una entitat indestructible
(Però, per definició Déu no pot destruir una entitat indestructible. La conclusió [15] és una contradicció. L'argument és una «reducció a l'absurd» que prova que les premisses 1-6 són inconsistents entre si).
_____________________________________________________________
| Pres de W. Neblet, Sherlock's Logic, University Press of America, Lanham-Nova York-Londres 1985, p. 127-128 trad. catal.: La lògica de Sherlock Holmes, La Magrana, Barcelona 1989, p. 125-126). |
Històricament, l'ús de raonaments indirectes és normal en geometria; les paradoxes de Zenó han estat contemplades també com a raonaments per reducció a l'absurd.
L'esquema lògic d'una reducció a l'absurd és el següent:
| [math]\displaystyle{
p\\
.\\
.\\
.\\
q\wedge \neg q\\ }[/math]
____________ [math]\displaystyle{ \neg p }[/math] |
Això vol dir que si suposem p i finalment arribem a una contradicció com [math]\displaystyle{ q\wedge \neg q }[/math], llavors hem de concloure la negació de la suposició p, per tant [math]\displaystyle{ \neg p }[/math] |
Suposem que es vol demostrar que «Raül no és magnànim» a partir de les premisses:
1. No és possible que Raül sigui magnànim i sever al mateix temps.
2. Si Raül és magnànim, perdona.
3. O Raül és sever o no perdona.
Veg. Apagoge.