Diferència entre revisions de la pàgina «Modus tollens»
De Wikisofia
m (bot: -veure exemple +veg. exemple) |
|||
| Línia 1: | Línia 1: | ||
{{ConcepteWiki}} | {{ConcepteWiki}} | ||
Expressió llatina que significa «manera que nega», i en la seva forma completa de ''modus tollendo tollens'', manera «que nega negant», i que s'aplica a la [[inferència, regles d'|regla d'inferència]] de [[lògica|lògica d'enunciats]], que té el següent esquema: | Expressió llatina que significa «manera que nega», i en la seva forma completa de ''modus tollendo tollens'', manera «que nega negant», i que s'aplica a la [[inferència, regles d'|regla d'inferència]] de [[lògica|lògica d'enunciats]], que té el següent esquema: | ||
| + | |||
| + | <center>Si P, llavors Q</center> | ||
| + | |||
| + | <center>No Q</center> | ||
| + | |||
| + | <center> _____________________ </center> | ||
| + | |||
| + | <center> No P</center> | ||
| + | |||
| + | |||
| + | El seu esquema lògic és: | ||
| + | |||
| + | <math>P \rightarrow{Q}</math> | ||
| + | |||
| + | <math>¬Q</math> | ||
| + | |||
| + | __________________________ | ||
| + | |||
| + | <math>¬P</math> | ||
| + | |||
| − | |||
| − | |||
<center>'''veg. exemple ↓'''</center> | <center>'''veg. exemple ↓'''</center> | ||
| − | + | ||
| + | |||
:Si Déu no existís tot estaria permès | :Si Déu no existís tot estaria permès | ||
: | : | ||
| Línia 28: | Línia 47: | ||
[[File:e5021-1.gif]] | [[File:e5021-1.gif]] | ||
| − | + | ||
Revisió del 20:07, 8 feb 2020
Expressió llatina que significa «manera que nega», i en la seva forma completa de modus tollendo tollens, manera «que nega negant», i que s'aplica a la regla d'inferència de lògica d'enunciats, que té el següent esquema:
El seu esquema lògic és:
[math]\displaystyle{ P \rightarrow{Q} }[/math]
[math]\displaystyle{ ¬Q }[/math]
__________________________
[math]\displaystyle{ ¬P }[/math]
- Si Déu no existís tot estaria permès
- Però no és veritat que tot estigui permès
- ___________________________________________
- Per tant, Déu existeix (Dostoyevsky)
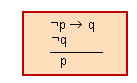
l'esquema lògic del qual és
[math]\displaystyle{ ¬p \rightarrow{q} }[/math]
[math]\displaystyle{ ¬q }[/math]
__________________________________
[math]\displaystyle{ p }[/math]