Diferència entre revisions de la pàgina «Esquema lògic d'una reducció a l'absurd»
De Wikisofia
m (Text de reemplaçament - "Raúl" a "Raül") |
|||
| (Hi ha 7 revisions intermèdies del mateix usuari que no es mostren) | |||
| Línia 1: | Línia 1: | ||
{{ConcepteWiki}} | {{ConcepteWiki}} | ||
L'esquema lògic d'una reducció a l'absurd és el següent: | L'esquema lògic d'una reducció a l'absurd és el següent: | ||
| + | {|class="wikitable" style="width: 30%;" | ||
| + | | style="width: 10%"|<math> | ||
| + | p\\ | ||
| + | .\\ | ||
| + | .\\ | ||
| + | .\\ | ||
| + | q\wedge \neg q\\ </math> | ||
| + | ____________ | ||
| − | < | + | <math> |
| − | + | \neg p | |
| + | </math> | ||
| + | | style="width: 50%"|Això vol dir que si suposem ''p'' i finalment arribem a una contradicció com <math>q\wedge \neg q</math>, llavors hem de concloure la negació de la suposició ''p'', per tant <math>\neg p</math> | ||
| + | |} | ||
| + | ---- | ||
Suposem que es vol demostrar que «Raül no és magnànim» a partir de les premisses: | Suposem que es vol demostrar que «Raül no és magnànim» a partir de les premisses: | ||
| Línia 13: | Línia 25: | ||
3. O Raül és sever o no perdona. | 3. O Raül és sever o no perdona. | ||
| − | + | [[Image:E3149-1Bcat.png|300px]] | |
{{Etiqueta | {{Etiqueta | ||
Revisió de 11:20, 5 oct 2018
L'esquema lògic d'una reducció a l'absurd és el següent:
| [math]\displaystyle{
p\\
.\\
.\\
.\\
q\wedge \neg q\\ }[/math]
____________ [math]\displaystyle{ \neg p }[/math] |
Això vol dir que si suposem p i finalment arribem a una contradicció com [math]\displaystyle{ q\wedge \neg q }[/math], llavors hem de concloure la negació de la suposició p, per tant [math]\displaystyle{ \neg p }[/math] |
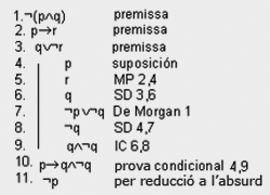
Suposem que es vol demostrar que «Raül no és magnànim» a partir de les premisses:
1. No és possible que Raül sigui magnànim i sever al mateix temps.
2. Si Raül és magnànim, perdona.
3. O Raül és sever o no perdona.