Diferència entre revisions de la pàgina «Esquema lògic d'una reducció a l'absurd»
De Wikisofia
| Línia 2: | Línia 2: | ||
L'esquema lògic d'una reducció a l'absurd és el següent: | L'esquema lògic d'una reducció a l'absurd és el següent: | ||
| − | + | <math> | |
p\\ | p\\ | ||
.\\ | .\\ | ||
| Línia 8: | Línia 8: | ||
.\\ | .\\ | ||
q\wedge \neg q\\ | q\wedge \neg q\\ | ||
| − | + | </math> | |
| + | ____________ | ||
| + | |||
| + | <math> | ||
\neg p | \neg p | ||
| − | </math | + | </math> |
| − | |||
| − | |||
| − | |||
| − | |||
Revisió del 23:18, 3 oct 2018
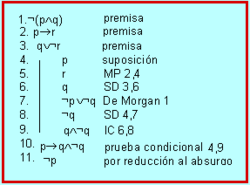
L'esquema lògic d'una reducció a l'absurd és el següent:
[math]\displaystyle{ p\\ .\\ .\\ .\\ q\wedge \neg q\\ }[/math] ____________
[math]\displaystyle{ \neg p }[/math]
Suposem que es vol demostrar que «Raül no és magnànim» a partir de les premisses:
1. No és possible que Raül sigui magnànim i sever al mateix temps.
2. Si Raül és magnànim, perdona.
3. O Raül és sever o no perdona.