Diferència entre revisions de la pàgina «Equivalència lògica»
De Wikisofia
| (Hi ha 3 revisions intermèdies del mateix usuari que no es mostren) | |||
| Línia 1: | Línia 1: | ||
{{ConcepteWiki}} | {{ConcepteWiki}} | ||
| − | + | Propietat d'aquelles [[fórmula|fórmules]] que són vertaderes o falses per a idèntiques assignacions de valors de veritat | |
| − | <center>[[ | + | <div class='mw-collapsible mw-collapsed'> |
| + | <center>'''veg. exemple ↓'''</center> | ||
| + | <div class="mw-collapsible-content"> | ||
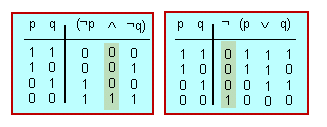
| + | <center><math>(¬p \wedge ¬q)</math> i <math>¬(p \vee q)</math></center> | ||
| + | |||
| + | |||
| + | <center>són fórmules equivalents:</center> | ||
| + | |||
| + | |||
| + | <center>[[File:e5010-3.gif]]</center> | ||
| + | |||
| + | [[Recurs:Exemple lògic de fórmules equivalents]] | ||
| + | </div></div> | ||
| + | |||
| + | En lògica de relacions són equivalents aquelles relacions que tenen la propietat de ser reflexives, simètriques i transitives (entenent que tota [[relació|relació]] que és simètrica i transitiva és també reflexiva). Les relacions d'equivalència permeten la [[classificació|classificació]]: [[partició|partició]] en grups mútuament excloents. | ||
| + | |||
| + | ---- | ||
| + | |||
| + | En [[lògica|lògica d'enunciats]] l'equivaència ve donada pel [[bicondicional|bicondicional]], el signe del qual és: <math>\leftrightarrow{}</math> i que es llegeix «si, i només si» | ||
| + | |||
| + | Se simbolitza com | ||
| + | |||
| + | '''<big><big><center><math>p\leftrightarrow q</math></center></big></big>''' | ||
Es llegeix, "P si, i només si, Q" | Es llegeix, "P si, i només si, Q" | ||
| Línia 8: | Línia 30: | ||
La seva taula de veritat és: | La seva taula de veritat és: | ||
| − | <center> | + | <center> |
| + | {|class="wikitable" style="width: 15%;" | ||
| + | |+ Taula del bicondicional | ||
| + | |- | ||
| + | | style="width: 15%"|<math>p~q</math> | ||
| + | | style="width: 15%"|<math>p\leftrightarrow q</math> | ||
| + | |- | ||
| + | | 1 1 | ||
| + | |1 1 1 | ||
| + | |- | ||
| + | |1 0 | ||
| + | |1 0 0 | ||
| + | |- | ||
| + | |0 1 | ||
| + | |0 0 0 | ||
| + | |- | ||
| + | |0 0 | ||
| + | |0 1 0 | ||
| + | |} | ||
| + | </center> | ||
| + | |||
| − | + | «p si i només si q és veritable quan p i q són tots dos veritables o tots dos falsos; en els altres casos, és fals». | |
Revisió de 12:38, 29 set 2018
Propietat d'aquelles fórmules que són vertaderes o falses per a idèntiques assignacions de valors de veritat
En lògica de relacions són equivalents aquelles relacions que tenen la propietat de ser reflexives, simètriques i transitives (entenent que tota relació que és simètrica i transitiva és també reflexiva). Les relacions d'equivalència permeten la classificació: partició en grups mútuament excloents.
En lògica d'enunciats l'equivaència ve donada pel bicondicional, el signe del qual és: [math]\displaystyle{ \leftrightarrow{} }[/math] i que es llegeix «si, i només si»
Se simbolitza com
Es llegeix, "P si, i només si, Q"
La seva taula de veritat és:
| [math]\displaystyle{ p~q }[/math] | [math]\displaystyle{ p\leftrightarrow q }[/math] |
| 1 1 | 1 1 1 |
| 1 0 | 1 0 0 |
| 0 1 | 0 0 0 |
| 0 0 | 0 1 0 |
«p si i només si q és veritable quan p i q són tots dos veritables o tots dos falsos; en els altres casos, és fals».
Exemple:
Si p = ets feliç» i q = «estimes», l'enunciat «ets feliç si i només si estimes», o «ets feliç sempre que estimis» és veritat quan «ets feliç i estimes» i quan «ni ets feliç ni estimes», però és fals si és veritat una d'ambdues coses i no l'altra.