Bicondicional

Connectiva diàdica que opera entre dues enunciats o dues lletres d'enunciat. Se simbolitza com

i es llegeix «P si i només si Q».

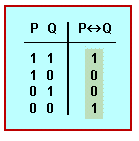
El seu sentit es precisa amb la seva definició mitjançant la taula de veritat:

[math]\displaystyle{ "P\leftrightarrow{Q}" }[/math] és veritable quan [math]\displaystyle{ P }[/math] i [math]\displaystyle{ Q }[/math] són tots dos veritables, en els altres casos és fals» (veg. exemple).

---

Exemple

Si p = ets feliç» i q = «estimes», l'enunciat «ets feliç si i només si mestresses», o «ets feliç sempre que estimis» és veritat quan «ets feliç i mestresses» i quan «ni ets feliç ni mestresses», però és fals si és veritat una d'ambdues coses i no l'altra.

---

Dos enunciats qualssevol, p i q, units per aquesta connectiva diàdica es llegeixen de diverses maneres, amb sentit no obstant això idèntic:

[math]\displaystyle{ (p\leftrightarrow{q}) }[/math]

pot llegir-se com: «p si i només si q», «si p llavors q i si q, llavors p», «p és condició necessària i suficient de q», «p equival a q», «si p llavors q i si no p, llavors no q»

---

Exemple

[math]\displaystyle{ (p\rightarrow{q})\wedge (q\rightarrow{p}) }[/math]
La seva taula de veritat és equivalent a la de
[math]\displaystyle{ (p\leftrightarrow{q}) }[/math]

[math]\displaystyle{ (p\rightarrow{q})\wedge (¬q\rightarrow{¬p}) }[/math]

La seva taula de veritat és equivalent a la de
[math]\displaystyle{ (p\leftrightarrow{q}) }[/math]

---