Diferència entre revisions de la pàgina «Lògica: exemple d'arbres lògics»
De Wikisofia
m (Text de reemplaçament - "Raúl" a "Raül") |
|||
| (2 revisions intermèdies per un altre usuari que no es mostra) | |||
| Línia 1: | Línia 1: | ||
{{RecursWiki | {{RecursWiki | ||
|Tipus=Exemple | |Tipus=Exemple | ||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
}} | }} | ||
{{RecursBase | {{RecursBase | ||
| Línia 19: | Línia 11: | ||
Sigui el raonament següent: | Sigui el raonament següent: | ||
| − | «Quan Anna canta, l'acompanya Raül o ho fa | + | «Quan n'Anna canta, l'acompanya en Raül o ho fa en Joel. Però avui no l'acompanya en Raül, per tant, ja que en Joel tampoc l'acompanya, n'Anna no canta». |
Que pot formalitzar-se de la següent manera: | Que pot formalitzar-se de la següent manera: | ||
| Línia 50: | Línia 42: | ||
Prou una sola combinació de valors que facin inconsistent el conjunt perquè disposem d'un contraexemple que fa invàlid el raonament (en aquest cas, p = 0 o 1, q = 1, r = 1, s = 0, t = 0. | Prou una sola combinació de valors que facin inconsistent el conjunt perquè disposem d'un contraexemple que fa invàlid el raonament (en aquest cas, p = 0 o 1, q = 1, r = 1, s = 0, t = 0. | ||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
{{InfoWiki}} | {{InfoWiki}} | ||
Revisió de 14:15, 5 set 2015
Exemple 3:
Sigui el raonament següent:
«Quan n'Anna canta, l'acompanya en Raül o ho fa en Joel. Però avui no l'acompanya en Raül, per tant, ja que en Joel tampoc l'acompanya, n'Anna no canta».
Que pot formalitzar-se de la següent manera:
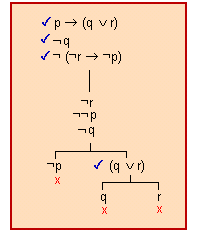
El seu arbre lògic és:
El conjunt format per les premisses donades i la negació de la conclusió (el contraexemple) és inconsistent; per tant el raonament és vàlid.
En canvi, en el següent cas, el raonament no és vàlid:
Sigui
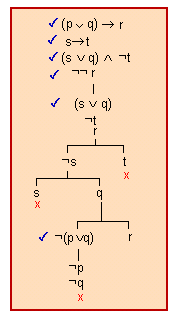
El seu arbre lògic és:
La branca en què es troba r no està tancada; per tant, el conjunt format per les premisses i la negació de la conclusió no és inconsistent. Per tant, el conjunt donat
és inconsistent, i la branca que queda sense tancar inclou els valors del contraexemple.
Prou una sola combinació de valors que facin inconsistent el conjunt perquè disposem d'un contraexemple que fa invàlid el raonament (en aquest cas, p = 0 o 1, q = 1, r = 1, s = 0, t = 0.