Diferència entre revisions de la pàgina «Quantificador»
De Wikisofia
m (Text de reemplaçament - "mático" a "màtic") |
m (Text de reemplaçament - "áticas" a "àtiques") |
||
| Línia 1: | Línia 1: | ||
{{ConcepteWiki}} | {{ConcepteWiki}} | ||
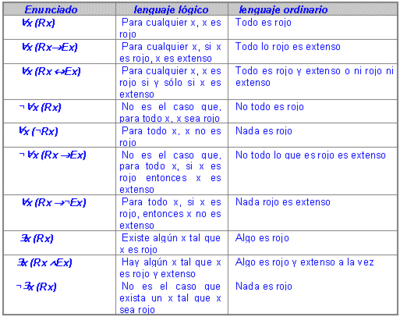
| − | En la lògica tradicional aristotèlica, les partícules [[sincategoremàtic| | + | En la lògica tradicional aristotèlica, les partícules [[sincategoremàtic|sincategoremàtiques]] «tots», «cap», «algun» i «algun...no», o equivalents, que afegides a un [[subjecte |subjecte]] i a un [[predicat|predicat]] units amb la [[còpula|còpula]] «és» donen lloc a [[categoremàtic|enunciats categoremàtics]], que poden ser universals o particulars([[enunciats AEIO|veure exemple]]). En la [[lògica|lògica de predicats]] de primer ordre, operadors que, afegits a una [[funció proposicional|funció proposicional,]] la transformen en un [[enunciat|enunciat]]. |
Són dos: el quantificador ''existencial'', que se simbolitza com a x i es llegeix «existeix almenys un x tal que...», amb el que s'afirma l'existència d'almenys un membre de la classe que descriu la funció, i el quantificador ''universal'', simbolitzat per x, que es llegeix «per a tot x...», i que afirma que tot és de la classe que descriu la funció. | Són dos: el quantificador ''existencial'', que se simbolitza com a x i es llegeix «existeix almenys un x tal que...», amb el que s'afirma l'existència d'almenys un membre de la classe que descriu la funció, i el quantificador ''universal'', simbolitzat per x, que es llegeix «per a tot x...», i que afirma que tot és de la classe que descriu la funció. | ||
Revisió del 22:50, 25 març 2015
En la lògica tradicional aristotèlica, les partícules sincategoremàtiques «tots», «cap», «algun» i «algun...no», o equivalents, que afegides a un subjecte i a un predicat units amb la còpula «és» donen lloc a enunciats categoremàtics, que poden ser universals o particulars(veure exemple). En la lògica de predicats de primer ordre, operadors que, afegits a una funció proposicional, la transformen en un enunciat.
Són dos: el quantificador existencial, que se simbolitza com a x i es llegeix «existeix almenys un x tal que...», amb el que s'afirma l'existència d'almenys un membre de la classe que descriu la funció, i el quantificador universal, simbolitzat per x, que es llegeix «per a tot x...», i que afirma que tot és de la classe que descriu la funció.